题目内容
16.已知函数f(x)=x3-3x,若对于区间[-3,2]上任意的x1,x2都有|f(x1)-f(x2)|≤t,则实数t的最小值是20.分析 求出f(x)的导数和极值,以及区间端点处的函数值,比较可得最值,即可得到|f(x1)-f(x2)|的最大值,进而得到t的范围,可得所求最小值.
解答 解:函数f(x)=x3-3x的导数为f′(x)=3x2-3,
令f′(x)=0,解得x=±1,
所以1,-1为函数f(x)的极值点.
因为f(-3)=-18,f(-1)=2,f(1)=-2,f(2)=2,
所以在区间[-3,2]上,f(x)max=2,f(x)min=-18,
所以对于区间[-3,2]上任意的x1,x2,|f(x1)-f(x2)|≤20,
所以t≥20,从而t的最小值为20.
故答案为:20.
点评 本题考查函数的最值的求法,注意运用导数,求极值和区间端点处的函数值,考查转化思想和运算能力,属于中档题.

练习册系列答案
相关题目
5.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+2≥0}\\{x-y+3≥0}\\{2x+y-3≤0}\end{array}\right.$,则目标函数z=x+2y的最大值为( )
| A. | 6 | B. | $\frac{3}{2}$ | C. | 0 | D. | 12 |
4.已知椭圆C:$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1的左、右焦点分别为F1,F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于直线l1于点P,线段PF2的垂直平分线与l1的交点的轨迹为曲线C2,若点Q是C2上任意的一点,定点A(4,3),B(1,0),则|QA|+|QB|的最小值为( )
| A. | 6 | B. | 3$\sqrt{3}$ | C. | 4 | D. | 5 |
1.有一段演绎推理:若直线平行于平面,则这条直线平行于平面内所有直线;≠已知直线b∥平面α,直线a?平面α;则直线b∥直线a”下列叙述正确的是( )
| A. | 该命题是真命题 | |
| B. | 该命题是假命题,因为大前提是错误的 | |
| C. | 该命题是假命题,因为小前提是错误的 | |
| D. | 该命题是假命题,因为结论是错误的 |
5.已知(x2+2x+3y)5的展开式中x5y2( )
| A. | 60 | B. | 180 | C. | 520 | D. | 540 |
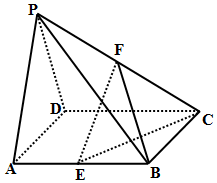 如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.