题目内容
8.已知α,β是两个不同的平面,m,n是两条不同的直线,给出了下列命题:①若m⊥α,m?β,则α⊥β;
②若m⊥n,m⊥α,则n∥α;
③若m∥α,α⊥β,则m⊥β,
④若α∩β=m,n∥m,且n?α,n?β,则n∥α,n∥β( )
| A. | ②④ | B. | ①②④ | C. | ①④ | D. | ①③ |
分析 在①中,由面面垂直的判定定理得α⊥β;在②中,n∥α或n?α;在③中,m与β相交、平行或m?β;在④中,由线面平行的判定定理得n∥α,n∥β.
解答 解:由α,β是两个不同的平面,m,n是两条不同的直线,知:
①若m⊥α,m?β,则由面面垂直的判定定理得α⊥β,故①正确;
②若m⊥n,m⊥α,则n∥α或n?α,故②错误;
③若m∥α,α⊥β,则m与β相交、平行或m?β,故③错误;
④若α∩β=m,n∥m,且n?α,n?β,
则由线面平行的判定定理得n∥α,n∥β,故④正确.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
16.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且a=1,b=2,c=$\sqrt{7}$,则∠C=( )
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
3.已知椭圆标准方程x2+$\frac{{y}^{2}}{10}$=1,则椭圆的焦点坐标为( )
| A. | ($\sqrt{10}$,0)(-$\sqrt{10}$,0) | B. | (0,$\sqrt{10}$),(0,-$\sqrt{10}$) | C. | (0,3)(0,-3) | D. | (3,0),(-3,0) |
13.下列式子恒成立的是( )
| A. | sin(α+β)=sinα+sinβ | B. | cos(α-β)=cosαcosβ+sinαsinβ | ||
| C. | sin(α-β)=cosαcosβ-sinαsinβ | D. | cos(α+β)=cosαsinβ-sinαcosβ |
17.已知向量$\overrightarrow{{A}{B}}$、$\overrightarrow{{A}C}$、$\overrightarrow{{A}D}$满足$\overrightarrow{{A}C}=\overrightarrow{{A}{B}}+\overrightarrow{{A}D}$,$|{\overrightarrow{{A}{B}}}|=2$,$|{\overrightarrow{{A}D}}|=1$,E、F分别是线段BC、CD的中点.若$\overrightarrow{D{E}}•\overrightarrow{{B}F}=-\frac{5}{4}$,则向量$\overrightarrow{{A}{B}}$与向量$\overrightarrow{{A}D}$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
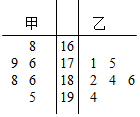 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图: