题目内容
3．已知椭圆标准方程x2+$\frac{{y}^{2}}{10}$=1，则椭圆的焦点坐标为（ ）| A． | （$\sqrt{10}$，0）（-$\sqrt{10}$，0） | B． | （0，$\sqrt{10}$），（0，-$\sqrt{10}$） | C． | （0，3）（0，-3） | D． | （3，0），（-3，0） |
分析 根据题意，由椭圆标准方程分析可得该椭圆的焦点在y轴上，进而可得c的值，由椭圆的焦点坐标公式可得答案．
解答 解：根据题意，椭圆标准方程x2+$\frac{{y}^{2}}{10}$=1，
则其焦点在y轴上，且c=$\sqrt{10-1}$=3，
则椭圆的焦点坐标为（0，3）和（0，-3），
故选：C．
点评 本题考查椭圆的简单几何性质，解题时注意该椭圆的焦点在y轴上．
练习册系列答案
相关题目
11．已知命题p：?x＞0，x+$\frac{1}{x}$≥2，命题q：?φ0＞0，使f（x）=sin（-2x+φ0）是偶函数，下列正确的是（ ）
| A． | p是假命题 | B． | ￢q是假命题 | C． | p∧（￢q）是真命题 | D． | （￢p）∨q是假命题 |
18．
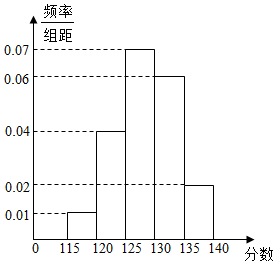某校在一次高三年级“诊断性”测试后，对该年级的500名考生的成绩进行统计分析，成绩的频率分布表及频率分布直方图如图所示，规定成绩不小于125分为优秀．
（1）若用分层抽样的方法从这500人中抽取20人的成绩进行分析，求其中成绩为优秀的学生人数；
（2）在（1）中抽取的20名学生中，要随机抽取2名学生参加分析座谈会，记其中成绩为优秀的人数为X，求X的分布列及数学期望．
某校在一次高三年级“诊断性”测试后，对该年级的500名考生的成绩进行统计分析，成绩的频率分布表及频率分布直方图如图所示，规定成绩不小于125分为优秀．（1）若用分层抽样的方法从这500人中抽取20人的成绩进行分析，求其中成绩为优秀的学生人数；
（2）在（1）中抽取的20名学生中，要随机抽取2名学生参加分析座谈会，记其中成绩为优秀的人数为X，求X的分布列及数学期望．
| 区间 | 人数 |
| [115，120） | 25 |
| [120，125） | a |
| [125，130） | 175 |
| [130，135） | 150 |
| [135，140） | b |
8．已知α，β是两个不同的平面，m，n是两条不同的直线，给出了下列命题：
①若m⊥α，m?β，则α⊥β；
②若m⊥n，m⊥α，则n∥α；
③若m∥α，α⊥β，则m⊥β，
④若α∩β=m，n∥m，且n?α，n?β，则n∥α，n∥β（ ）
①若m⊥α，m?β，则α⊥β；
②若m⊥n，m⊥α，则n∥α；
③若m∥α，α⊥β，则m⊥β，
④若α∩β=m，n∥m，且n?α，n?β，则n∥α，n∥β（ ）
| A． | ②④ | B． | ①②④ | C． | ①④ | D． | ①③ |
15．已知cosα=-$\frac{1}{2}$，且α是钝角，则tanα等于（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | -$\sqrt{3}$ | D． | -$\frac{\sqrt{3}}{3}$ |
12．某市小型机动车驾照“科二”考试共有5项考察项目，分别记作①，②，③，④，⑤
（Ⅰ）某教练将所带10名学员“科二”模拟考试成绩进行统计（如表所示），并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测（只测不合格项目），求补测项目种类不超过3项的概率．
（Ⅱ）“科二”考试中，学员需缴纳150元报名费，并进行1轮测试（按①，②，③，④，⑤的顺序进行），如果某项目不合格，可免费再进行1轮补测，若第1轮补测中仍有不合格项目，可选择“是否补考”，若补考则需缴纳300元补考费，并获得最多2轮补考机会，否则考试结束．每1轮补测都按①，②，③，④，⑤的顺序进行．学员在任何1轮测试或补测中5个项目均合格，方可通过“科二”考试，每人最多只能补考1次．某学员每轮测试或补测通过①，②，③，④，⑤各项测试的概率依次为1，1，1，$\frac{9}{10}$，$\frac{2}{3}$，且他遇到“是否补考”的决断时会选择补考．
（Ⅰ）求该学员能通过“科二”考试的概率．
（Ⅱ）求该学员缴纳的考试费用X的数学期望．
（Ⅰ）某教练将所带10名学员“科二”模拟考试成绩进行统计（如表所示），并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测（只测不合格项目），求补测项目种类不超过3项的概率．
（Ⅱ）“科二”考试中，学员需缴纳150元报名费，并进行1轮测试（按①，②，③，④，⑤的顺序进行），如果某项目不合格，可免费再进行1轮补测，若第1轮补测中仍有不合格项目，可选择“是否补考”，若补考则需缴纳300元补考费，并获得最多2轮补考机会，否则考试结束．每1轮补测都按①，②，③，④，⑤的顺序进行．学员在任何1轮测试或补测中5个项目均合格，方可通过“科二”考试，每人最多只能补考1次．某学员每轮测试或补测通过①，②，③，④，⑤各项测试的概率依次为1，1，1，$\frac{9}{10}$，$\frac{2}{3}$，且他遇到“是否补考”的决断时会选择补考．
（Ⅰ）求该学员能通过“科二”考试的概率．
（Ⅱ）求该学员缴纳的考试费用X的数学期望．
| 项目/学号编号 | ① | ② | ③ | ④ | ⑤ |
| （1） | T | T | T | ||
| （2） | T | T | T | ||
| （3） | T | T | T | T | |
| （4） | T | T | T | ||
| （5） | T | T | T | T | |
| （6） | T | T | T | ||
| （7） | T | T | T | T | |
| （8） | T | T | T | T | T |
| （9） | T | T | T | ||
| （10） | T | T | T | T | T |
| 注：“T”表示合格，空白表示不合格 | |||||