题目内容
15.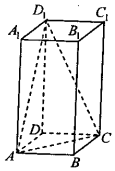 在正四棱柱ABCD-A1B1C1D1中,AB=2,BB1=4,则BB1与平面ACD1所成角的正弦值为( )
在正四棱柱ABCD-A1B1C1D1中,AB=2,BB1=4,则BB1与平面ACD1所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
分析 如图所示,建立空间直角坐标系.设平面ACD1的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=0}\\{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=0}\end{array}\right.$,设BB1与平面ACD1所成角为θ,利用sinθ=|$cos<\overrightarrow{n},\overrightarrow{B{B}_{1}}>$|=$\frac{|\overrightarrow{n}•\overrightarrow{B{B}_{1}}|}{|\overrightarrow{n}||\overrightarrow{B{B}_{1}}|}$即可得出.
解答 解:如图所示,建立空间直角坐标系.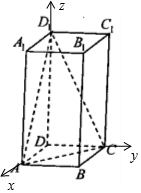
则D(0,0,0),A(2,0,0),C(0,2,0),D1(0,0,4),
B(2,2,0),B1(2,2,4),$\overrightarrow{AC}$=(-2,2,0),$\overrightarrow{A{D}_{1}}$=(-2,0,4),
$\overrightarrow{B{B}_{1}}$=(0,0,4).
设平面ACD1的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=0}\\{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{-2x+2y=0}\\{-2x+4z=0}\end{array}\right.$,
取$\overrightarrow{n}$=(2,2,1),
设BB1与平面ACD1所成角为θ,
则sinθ=|$cos<\overrightarrow{n},\overrightarrow{B{B}_{1}}>$|=$\frac{|\overrightarrow{n}•\overrightarrow{B{B}_{1}}|}{|\overrightarrow{n}||\overrightarrow{B{B}_{1}}|}$=$\frac{4}{\sqrt{9}×4}$=$\frac{1}{3}$.
故选:A.
点评 本题考查了空间位置关系、空间角、法向量的应用、向量夹角公式,考查了数形结合方法、推理能力与计算能力,属于中档题.

| A. | $\frac{1}{6}$,$\frac{1}{6}$ | B. | $\frac{1}{2}$,$\frac{2}{3}$ | C. | $\frac{1}{6}$,$\frac{2}{3}$ | D. | $\frac{2}{3}$,$\frac{1}{2}$ |
| A. | (-∞,-5)∪(5,+∞) | B. | (-5,-2)∪(2,5) | C. | (-∞,-5)∪(-2,0) | D. | (-∞,-5)∪(-2,0)∪(2,5) |
| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{8}{15}$ | D. | $\frac{3}{5}$ |
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | -$\frac{1}{4}$ |
| A. | {m|m>$\frac{9}{4}$} | B. | {m|m≥$\frac{9}{4}$} | C. | {m|m<$\frac{9}{4}$} | D. | {m|m≤$\frac{9}{4}$} |
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |