题目内容
4．已知x＞0，y＞0且x+y=4，若不等式$\frac{1}{x}$+$\frac{4}{y}$≥m恒成立，则m的取值范围是（ ）| A． | {m|m＞$\frac{9}{4}$} | B． | {m|m≥$\frac{9}{4}$} | C． | {m|m＜$\frac{9}{4}$} | D． | {m|m≤$\frac{9}{4}$} |
分析 利用“乘1法”与基本不等式的性质求解$\frac{1}{x}$+$\frac{4}{y}$的最小值可得答案．
解答 解：x＞0，y＞0且x+y=4，
则：$\frac{x}{4}+\frac{y}{4}=1$，
那么（$\frac{1}{x}$+$\frac{4}{y}$）（$\frac{x}{4}+\frac{y}{4}$）=$\frac{1}{4}$+1$+\frac{x}{y}+\frac{y}{4x}$≥$\frac{5}{4}$$+2\sqrt{\frac{x}{y}•\frac{y}{4x}}$=$\frac{9}{4}$，当且仅当2x=y=$\frac{8}{3}$时取等号．
∴$\frac{1}{x}$+$\frac{4}{y}$的最小值为$\frac{9}{4}$．
要使不等式$\frac{1}{x}$+$\frac{4}{y}$≥m恒成立，
∴m$≤\frac{9}{4}$．
故选D．
点评 本题考查了“乘1法”与基本不等式的性质的运用，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数f（x）是R上的奇函数，且当x＞0时，函数的解析式为f（x）=log2（x+1）．
15．
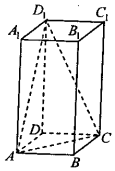在正四棱柱ABCD-A1B1C1D1中，AB=2，BB1=4，则BB1与平面ACD1所成角的正弦值为（ ）
在正四棱柱ABCD-A1B1C1D1中，AB=2，BB1=4，则BB1与平面ACD1所成角的正弦值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
19．椭圆$\frac{{x}^{2}}{4}$+y2=1的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | 2 |
9．已知m，n为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的有（ ）
（1）m?α，n?α，m∥β，n∥β⇒α∥β （2）n∥m，n⊥α⇒m⊥α
（3）α∥β，m?α，n?β⇒m∥n （4）m⊥α，m⊥n⇒n∥α
（1）m?α，n?α，m∥β，n∥β⇒α∥β （2）n∥m，n⊥α⇒m⊥α
（3）α∥β，m?α，n?β⇒m∥n （4）m⊥α，m⊥n⇒n∥α
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
16．若向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为（ ）
| A． | （1，5） | B． | （1，1） | C． | （3，1） | D． | （3，5） |
13．已知函数f（x）=（x2-4）（x-a），a为实数，f′（1）=0，则f（x）在[-2，2]上的最大值是（ ）
| A． | $\frac{9}{2}$ | B． | 1 | C． | $\frac{3}{5}$ | D． | $\frac{50}{27}$ |