下列函数①y=2x,②y=log0.5(x+1),③y=$\sqrt{x}$,④y=|x-1|.其中在区间(0.1)上单调递减的函数的序号是( )A．①③B．②③C．①④D．②④ 题目和参考答案——青夏教育精英家教网—

题目内容

3．下列函数①y=2^x；②y=log_0.5（x+1）；③y=$\sqrt{x}$；④y=|x-1|，其中在区间（0，1）上单调递减的函数的序号是（　　）

A．

①③

B．

②③

C．

①④

D．

②④

分析逐一分析给定四个函数在区间（0，1）上的单调性，可得答案．

解答解：函数①y=2^x在区间（0，1）上单调递增；
②y=log_0.5（x+1）在区间（0，1）上单调递减；
③y=$\sqrt{x}$在区间（0，1）上单调递增；
④y=|x-1|在区间（0，1）上单调递减；
故选：D

点评本题考查的知识点是函数的单调性，熟练掌握各种基本初等函数的单调性，是解答的关键．

练习册系列答案

14．

函数f（x）是R上的奇函数，且当x＞0时，函数的解析式为f（x）=log₂（x+1）．
（1）求当x＜0时，函数的解析式；
（2）用分段函数形式写出函数f（x）在R上的解析式，并在坐标系中画出f（x）的草图．

11．函数f（x）=log_a（x-3a）与函数$g（x）={log_a}\frac{1}{x-a}$（a＞0，且a≠1）在给定区间[a+2，a+3]上有意义．
（1）求a的取值范围；
（2）若在给定区间[a+2，a+3]上恒有|f（x）-g（x）|≤1，求a的取值范围．

18．若i是虚数单位，则计算$\frac{1+7i}{2-i}$的结果为（　　）

8．一个几何体的三视图如图所示，则这个几何体的体积等于（　　）

15．

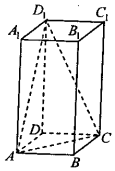在正四棱柱ABCD-A₁B₁C₁D₁中，AB=2，BB₁=4，则BB₁与平面ACD₁所成角的正弦值为（　　）

$\frac{2\sqrt{2}}{3}$

12．函数f（x）=x（x-m）²在x=1处取得极小值，则m=1．

13．已知函数f（x）=（x²-4）（x-a），a为实数，f′（1）=0，则f（x）在[-2，2]上的最大值是（　　）

试题分类