题目内容
7．已知抛物线y=ax2的准线方程为y=1，则a的值为（ ）| A． | 4 | B． | $\frac{1}{4}$ | C． | -4 | D． | -$\frac{1}{4}$ |
分析 利用抛物线的准线方程求解即可．
解答 解：抛物线y=ax2的准线方程为y=1，
∴-$\frac{1}{4a}$=1，
解得a=-$\frac{1}{4}$，
故选：D
点评 本题考查抛物线的简单性质的应用，基本知识的考查．
练习册系列答案
相关题目
18．若i是虚数单位，则计算$\frac{1+7i}{2-i}$的结果为（ ）
| A． | 1+3i | B． | 1-3i | C． | -1+3i | D． | -1-3i |
15．
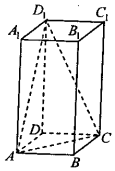在正四棱柱ABCD-A1B1C1D1中，AB=2，BB1=4，则BB1与平面ACD1所成角的正弦值为（ ）
在正四棱柱ABCD-A1B1C1D1中，AB=2，BB1=4，则BB1与平面ACD1所成角的正弦值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
如图，在救灾现场，搜救人员从A点出发沿正北方向行进x米到达B处，探测到一个生命迹象，然后从B处沿南偏东75°行进30米到达C处，探测到另一个生命迹象，如果C处恰好在A处的北偏东60°方向上，那么x=10$\sqrt{6}$．米．
19．椭圆$\frac{{x}^{2}}{4}$+y2=1的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | 2 |
16．若向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为（ ）
| A． | （1，5） | B． | （1，1） | C． | （3，1） | D． | （3，5） |
17．已知圆O：x2+y2+6x-2y+6=0，若斜率存在且不等于0的直线l过点A（4，0）且被圆O截得的弦长为2$\sqrt{3}$，则直线l的方程为（ ）
| A． | 24x+7y-28=0 | B． | 7x+24y-28=0 | C． | 24x-7y-28=0 | D． | 7x-24y-28=0 |