题目内容
20．设Sn为等差数列{an}的前n项和，若a1+2a4=a6，S3=3，则a9=15，S10=80．分析 利用等差数列的通项公式及前n项和公式，列出方程组，求出首项和公差，由此能求出结果．
解答 解：∵Sn为等差数列{an}的前n项和，a1+2a4=a6，S3=3，
∴$\left\{\begin{array}{l}{{a}_{1}+2（{a}_{1}+3d）={a}_{1}+5d}\\{3{a}_{1}+\frac{3×2}{2}d=3}\end{array}\right.$，
解得a1=-1，d=2，
∴a9=a1+8d=-1+16=15，
S10=$10{a}_{1}+\frac{10×9}{2}d=-10+90=80$．
故答案为：15，80．
点评 本题考查等差数列中第9项和前10项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
10．若点P（m-2，n+1），Q（n，m-1）关于直线l对称，则l的方程是（ ）
| A． | x-y+1=0 | B． | x-y=0 | C． | x+y+1=0 | D． | x+y=0 |
8．一个几何体的三视图如图所示，则这个几何体的体积等于（ ）
| A． | 6 | B． | 12 | C． | 18 | D． | 36 |
15．
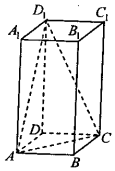在正四棱柱ABCD-A1B1C1D1中，AB=2，BB1=4，则BB1与平面ACD1所成角的正弦值为（ ）
在正四棱柱ABCD-A1B1C1D1中，AB=2，BB1=4，则BB1与平面ACD1所成角的正弦值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
5．若sinα=$\frac{4}{5}$，且α为锐角，则tanα的值等于（ ）
| A． | $\frac{4}{3}$ | B． | -$\frac{3}{4}$ | C． | $\frac{3}{4}$ | D． | -$\frac{4}{3}$ |
9．已知m，n为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的有（ ）
（1）m?α，n?α，m∥β，n∥β⇒α∥β （2）n∥m，n⊥α⇒m⊥α
（3）α∥β，m?α，n?β⇒m∥n （4）m⊥α，m⊥n⇒n∥α
（1）m?α，n?α，m∥β，n∥β⇒α∥β （2）n∥m，n⊥α⇒m⊥α
（3）α∥β，m?α，n?β⇒m∥n （4）m⊥α，m⊥n⇒n∥α
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
10．已知sinα=$\frac{1}{4}$，则cos2α的值为（ ）
| A． | -$\frac{7}{8}$ | B． | $\frac{7}{8}$ | C． | $\frac{1}{2}$ | D． | $\frac{15}{16}$ |