题目内容
13．${∫}_{-2}^{-1}$$\frac{2}{x}$dx=（ ）| A． | -ln2 | B． | ln2 | C． | -2ln2 | D． | 2ln2 |
分析 由${∫}_{-2}^{-1}$$\frac{2}{x}$dx=-${∫}_{1}^{2}$$\frac{2}{x}$dx，再根据定积分的计算法则计算即可．
解答 解：${∫}_{-2}^{-1}$$\frac{2}{x}$dx=-${∫}_{1}^{2}$$\frac{2}{x}$dx=-2lnx|${\;}_{1}^{2}$=-2ln2，
故选：C．
点评 本题考查了定积分的计算，关键是求出原函数，属于基础题．
练习册系列答案
相关题目
3．某洗衣机生产流水线上有三条不同的作业线，每条作业线上的质量指标分别为x，y，z，用综合指标S=x+y+z评价该洗衣机的等级．若S≥5，则该洗衣机为特等品；若4≤S≤5，则该洗衣机为一等品；若S＜4，则该洗衣机不合格．现从这一批洗衣机中，随机抽取10台作为样本，其质量指标列表如下：
（1）利用上表提供的样本数据估计该批产品的一等品率；
（2）从编号为A1到A6的6台洗衣机中，随机抽取2台，
①用产品编号列出所有可能的结果；
②设事件B为“在取出的2台洗衣机中，恰有一台是一等品一台不合格”，求事件B发生的概率．
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标（x，y，z） | （1，1，2） | （2，1，1） | （2，2，2） | （1，1，1） | （1，2，1） |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标（x，y，z） | （1，2，2） | （2，1，1） | （2，2，1） | （1，1，1） | （2，1，2） |
（2）从编号为A1到A6的6台洗衣机中，随机抽取2台，
①用产品编号列出所有可能的结果；
②设事件B为“在取出的2台洗衣机中，恰有一台是一等品一台不合格”，求事件B发生的概率．
4．f（x）=$\left\{\begin{array}{l}{\frac{\sqrt{x+1}-1}{x}，x≠0}\\{0，x=0}\end{array}\right.$，则x=0是（ ）
| A． | 可去间断点 | B． | 无穷间断点 | C． | 连续点 | D． | 跳跃间断点 |
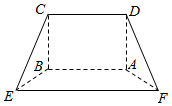如图，在多面体ABCDEF中，四边形ABCD是矩形，四边形ABEF为等腰梯形，且AB∥EF，AF=2，EF=2AB=4AD=4$\sqrt{2}$，平面ABCD⊥平面ABEF．
2．执行如图所示的程序框图，若输入x=1，则输出y的值是（ ）
| A． | 1 | B． | 3 | C． | 7 | D． | 15 |
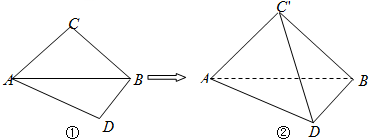
某次考试无纸化阅卷的评分规则的程序如图所示，x1，x2，x3为三个评卷人对同一道题的独立评分，p为该题的最终得分，当x1=6，x2=9，p=8.5时，x3=（ ）