题目内容
16.长方体ABCD-A1B1C1D1满足底面ABCD是边长为10的正方形,AA1=20,若在长方体内部(包括各面)存在一点P,使得|PA|+|PB|=26,则四棱锥P-ABCD的体积的最大值为400.分析 由题意画出图形,由题意可得,满足条件的P点在平面ABB1A1内,利用椭圆定义求出P的轨迹,得到到AB距离最大的P点到AB的距离为12,即四棱锥P-ABCD的高为12,然后代入棱锥体积公式得答案.
解答 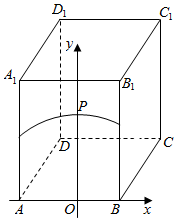 解:如图由题意可知,当P点位于平面ABB1A1上时,能使四棱锥P-ABCD的体积最大,
解:如图由题意可知,当P点位于平面ABB1A1上时,能使四棱锥P-ABCD的体积最大,
在平面ABB1A1内,以AB所在直线为x轴,以AB的垂直平分线为y轴建系,
∵AB=10,且|PA|+|PB|=26>10,
∴P在以A,B为焦点的椭圆上,
且a=13,c=5,∴b2=a2-c2=132-52=122,
则平面ABB1A1内,满足|PA|+|PB|=26,且到AB距离最大的P点到AB的距离为12,
∴四棱锥P-ABCD的体积的最大值为$\frac{1}{3}×10×10×12=400$.
故答案为:400.
点评 本题考查棱锥的体积,考查了数形结合的解题思想方法,利用椭圆定义求出满足条件的P点是解答该题的关键,是中档题.

练习册系列答案
相关题目
6.为了对某课题进行研究,用分层抽样的方法从三所高校A,B,C的相关人中抽取若干人组成研究小组,有关数据如下表(单位:人).
(1)求x,y;
(2)若从高校B,C抽取的人中选2人作专题发言,求这2人均来自高校C的概率.
| 高校 | 相关人数 | 抽取人数 |
| A | 54 | x |
| B | 36 | 2 |
| C | 72 | y |
(2)若从高校B,C抽取的人中选2人作专题发言,求这2人均来自高校C的概率.
7.已知函数$f(x)=\left\{{\begin{array}{l}{3+{{log}_2}x,x>0}\\{2{x^2}-3x,x≤0}\end{array}}\right.$,则不等式f(x)≤5的解集为( )
| A. | [-1,1] | B. | (-∞,-1]∪(0,1) | C. | [-1,4] | D. | (-∞,-1]∪[0,4] |
4.f(x)=$\left\{\begin{array}{l}{\frac{\sqrt{x+1}-1}{x},x≠0}\\{0,x=0}\end{array}\right.$,则x=0是( )
| A. | 可去间断点 | B. | 无穷间断点 | C. | 连续点 | D. | 跳跃间断点 |
11.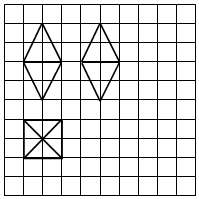 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |
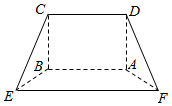 如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.
如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.