题目内容
14．若loga（3a-2）是正数，则实数a的取值范围是$（{\frac{2}{3}，1}）∪（{1，+∞}）$．分析 对底数a分类讨论结合对数函数的单调性可得a的不等式组，解不等式组综合可得．
解答 解：由题意可得loga（3a-2）是正数，
当a＞1时，函数y=logax在（0，+∞）单调递增，
则3a-2＞1，解得a＞1；
当0＜a＜1时，函数y=logax在（0，+∞）单调递减，
则0＜3a-2＜1，解得$\frac{2}{3}$＜a＜1；
综上可得实数a的取值范围为：$（{\frac{2}{3}，1}）∪（{1，+∞}）$
故答案为：$（{\frac{2}{3}，1}）∪（{1，+∞}）$
点评 本题考查对数函数的图象和性质，涉及分类讨论的思想，属基础题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
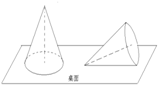用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥，放在水平桌面上，被一阵风吹倒，如图，则它的最高点到桌面的距离为5$\sqrt{3}$cm．
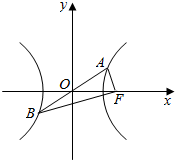如图，已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上有一点A，它关于原点的对称点为B，点F为是双曲线的右焦点，且满足AF⊥BF，设∠ABF=α，α∈[$\frac{π}{12}$，$\frac{π}{6}$]，则该双曲线离心率e的取值范围为[$\sqrt{2}$，$\sqrt{3}$+1]．
4．若无穷等差数列{an}的首项a1＞0，公差d＜0，{an}的前n项和为Sn，则（ ）
| A． | Sn单调递减 | B． | Sn单调递增 | C． | Sn有最大值 | D． | Sn有最小值 |