Question

19．某三棱椎的三视图如图所示，该三棱锥的四个面的面积中，最大的是4$\sqrt{7}$

Answer 1

分析 作出直观图，分别计算四个面的面积，得出答案．

解答 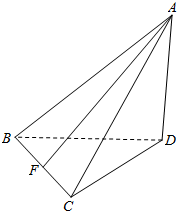解：由三视图可知该几何体是个底面是正三角形，棱AD⊥底面BCD的三棱锥，如图．其中AD=4，BD=4，取BC的中点F，
则DF=2$\sqrt{3}$，AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=2$\sqrt{7}$，
∴S_△ABC=$\frac{1}{2}×BC×AF$=4$\sqrt{7}$，S_△BCD=$\frac{\sqrt{3}}{4}×B{D}^{2}$=4$\sqrt{3}$，S_△ABD=$\frac{1}{2}×BD×AD$=8，S_△ACD=$\frac{1}{2}×CD×AD$=8，
故答案为4$\sqrt{7}$．

点评 本题考查了常见几何体的三视图和体积计算，作出直观图可方便计算．