题目内容
 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则 | BD |
| DA |
考点:与圆有关的比例线段
专题:直线与圆
分析:利用勾股定理求出AB=5,利用切割线定理求出BD=
=
,由此能求出
.
| BC2 |
| AB |
| 16 |
| 5 |
| BD |
| DA |
解答:
解:∵Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,
∴AB=
=5(cm),
∵以AC为直径的圆与AB交于点D,
∴BC2=BD•AB,∴BD=
=
,
∴DA=5-
=
,
∴
=
=
.
故答案为:
.
∴AB=
| 9+16 |

∵以AC为直径的圆与AB交于点D,
∴BC2=BD•AB,∴BD=
| BC2 |
| AB |
| 16 |
| 5 |
∴DA=5-
| 16 |
| 5 |
| 9 |
| 5 |
∴
| BD |
| DA |
| ||
|
| 16 |
| 9 |
故答案为:
| 16 |
| 9 |
点评:本题考查两条线段的比值的求法,是中档题,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知集合A={1,2,3},B={x|x≤2},则A∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |
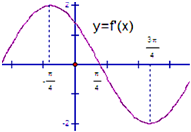 已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),其导函数f′(x)的部分图形如图所示,则函数f(x)的解析式( )
已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),其导函数f′(x)的部分图形如图所示,则函数f(x)的解析式( )A、f(x)=2sin(x+
| ||
B、f(x)=4sin(x+
| ||
C、f(x)=2sin(x+
| ||
D、f(x)=4sin(x+
|


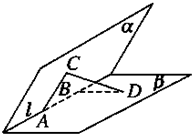 二面角α-l-β为60°,A、B是棱l上的两点,AC、BD分别在半平面α、β内,AC⊥l,BD⊥l,且AB=AC=a,BD=2a,则CD的长为
二面角α-l-β为60°,A、B是棱l上的两点,AC、BD分别在半平面α、β内,AC⊥l,BD⊥l,且AB=AC=a,BD=2a,则CD的长为