题目内容
函数y=2x+2-x的最小值为 .
考点:基本不等式,指数型复合函数的性质及应用
专题:不等式的解法及应用
分析:根据基本不等式的性质即可得到结论.
解答:
解:∵y=2x>0,
∴y=2x+2-x≥2
=2,
当且仅当2x=2-x,即x=-x,x=0时取等号,
故函数y=2x+2-x的最小值为2,
故答案为:2
∴y=2x+2-x≥2
| 2x•2-x |
当且仅当2x=2-x,即x=-x,x=0时取等号,
故函数y=2x+2-x的最小值为2,
故答案为:2
点评:本题主要考查基本不等式的应用,根据基本不等式成立的条件是解决本题的根据,比较基础.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
如图是计算
+
+
+…+
的值的一个程序框图,其中在判断框中应填入的条件是( )

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |

| A、i<10 | B、i>10 |
| C、i<20 | D、i>20 |
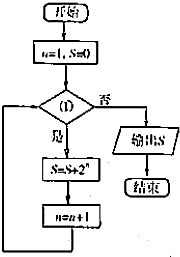 运行如图框图输出的S是254,则①应为
运行如图框图输出的S是254,则①应为 F.
F. 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则