题目内容
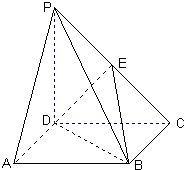 如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.(1)证明:PA∥平面BDE;
(2)证明:AD⊥平面PDC
(3)证明:DE⊥平面PBC.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)连结AC,设AC与BD交于O点,连结EO.由底面ABCD是正方形,可得OE∥PA,即可证明PA∥平面BDE.
(2先证DE⊥PC.由PD⊥底面ABCD,可证PD⊥AD,又由于AD⊥CD,PD∩CD=D,即可证AD⊥底面PCD.
(3)由(2)可知AD⊥DE.又由题意得AD∥BC,故BC⊥DE.于是,由BC∩PC=C,DE⊥PC,BC⊥DE可得DE⊥底面PBC.
(2先证DE⊥PC.由PD⊥底面ABCD,可证PD⊥AD,又由于AD⊥CD,PD∩CD=D,即可证AD⊥底面PCD.
(3)由(2)可知AD⊥DE.又由题意得AD∥BC,故BC⊥DE.于是,由BC∩PC=C,DE⊥PC,BC⊥DE可得DE⊥底面PBC.
解答:
 (本题满分12分)
(本题满分12分)
证明:(1)连结AC,设AC与BD交于O点,连结EO.
∵底面ABCD是正方形,∴0为AC的中点,又E为PC的中点,
∴OE∥PA,∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE.…(4分)
(2)∵PD=DC,E是PC的中点,∴DE⊥PC.
∵PD⊥底面ABCD,∴PD⊥AD.
又由于AD⊥CD,PD∩CD=D,故AD⊥底面PCD,…(8分)
(3)由(2)所以有AD⊥DE.又由题意得AD∥BC,故BC⊥DE.
于是,由BC∩PC=C,DE⊥PC,BC⊥DE可得DE⊥底面PBC.…(12分)
 (本题满分12分)
(本题满分12分)证明:(1)连结AC,设AC与BD交于O点,连结EO.
∵底面ABCD是正方形,∴0为AC的中点,又E为PC的中点,
∴OE∥PA,∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE.…(4分)
(2)∵PD=DC,E是PC的中点,∴DE⊥PC.
∵PD⊥底面ABCD,∴PD⊥AD.
又由于AD⊥CD,PD∩CD=D,故AD⊥底面PCD,…(8分)
(3)由(2)所以有AD⊥DE.又由题意得AD∥BC,故BC⊥DE.
于是,由BC∩PC=C,DE⊥PC,BC⊥DE可得DE⊥底面PBC.…(12分)
点评:本题主要考察了直线与平面平行的判定,直线与平面垂直的判定,属于基本知识的考查.

练习册系列答案
相关题目
关于直线的倾斜角与斜率,下列说法正确的是( )
| A、所有的直线都有倾斜角和斜率 |
| B、所有的直线都有倾斜角,但不一定都有斜率 |
| C、直线的倾斜角和斜率有时都不存在 |
| D、所有的直线都有斜率,但不一定有倾斜角 |
如图为某几何体的三视图,则该几何体的表面积为( )


A、10+
| ||||
B、10+
| ||||
C、6+2
| ||||
D、6+
|