题目内容
若函数f（x）=x3-bx+1有且仅有两个不同零点，则b的值为 ．
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：若函数f（x）恰好有两个不同的零点，等价为函数的极值为0，建立方程即可得到结论
解答：
解：∵函数f（x）=x3-bx+1，
∴f′（x）=3x2-b，
若b≤0，函数f′（x）=3x2-b≥0，此时f（x）单调递增，不满足条件，
若b＞0，由f′（x）=3x2-b=0得x=±
，可验证x=±
是函数f（x）的两个极值点，
若函数f（x）恰好有两个不同的零点，
则f（±
）=0，
∵f（0）=1＞0，∴只能有f（
）=0，
即（
）3-b（
）+1=0，
化简为b
•（-
）+1=0，
解得b=3•4 -
．
∴f′（x）=3x2-b，
若b≤0，函数f′（x）=3x2-b≥0，此时f（x）单调递增，不满足条件，
若b＞0，由f′（x）=3x2-b=0得x=±
| ||
| 3 |
| ||
| 3 |
若函数f（x）恰好有两个不同的零点，
则f（±
| ||
| 3 |
∵f（0）=1＞0，∴只能有f（
| ||
| 3 |
即（
| ||
| 3 |
| ||
| 3 |
化简为b
| 3 |
| 2 |
2
| ||
| 9 |
解得b=3•4 -
| 1 |
| 3 |
点评：本题主要考查函数零点的应用以及切线方程的求解，根据导数的几何意义是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
“非p为假命”是“p且q是真命题”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也木必要条件 |
定义在R上的函数f（x）满足：f（x）=f（4-x）且f（2-x）+f（x-2）=0，若f（2）=1，则f（2014）的值是（ ）
| A、-1 | B、0 | C、1 | D、无法确定 |
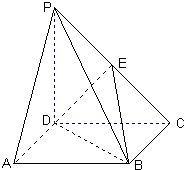如图，四棱锥P-ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=DC，E是PC的中点．