题目内容
如图为某几何体的三视图,则该几何体的表面积为( )


A、10+
| ||||
B、10+
| ||||
C、6+2
| ||||
D、6+
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体为一个四棱锥,如图所示,CD⊥底面PAD,BA⊥底面PAD,PA⊥AD,PA=AD=CD=2,AB=1.即可得出.
解答:
解:由三视图可知:该几何体为一个四棱锥,如图所示,CD⊥底面PAD,BA⊥底面PAD,PA⊥AD,PA=AD=CD=2,AB=1.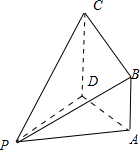
PC=2
,PB=
,BC=
.
∴S△PBC=
×2
×
=
.
该几何体的表面积S=
+
×2×1+
×2
×2+
×2×2+
=6+2
+
.
故选:C.

PC=2
| 3 |
| 5 |
| 5 |
∴S△PBC=
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
该几何体的表面积S=
| (1+2)×2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 6 |
=6+2
| 2 |
| 6 |
故选:C.
点评:本题考查了四棱锥的三视图及其表面积的计算公式、勾股定理,考查了计算能力,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知实数x,y满足
,则z=x+y的最小值等于( )
|
| A、0 | B、1 | C、2 | D、3 |
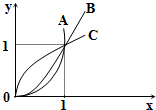 已知幂函数①y=x
已知幂函数①y=x | 1 |
| 2 |
| A、①②③ | B、③①② |
| C、③②① | D、①③② |
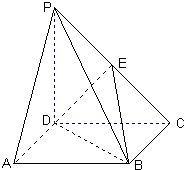 如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.