题目内容
4.已知三条不同的直线a,b,c,若a⊥b,则“a⊥c”是“b∥c”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据直线平行和垂直的关系 结合充分条件和必要条件的定义进行判断即可.
解答 解:垂直于同一条直线的两条直线不一定平行,
即当a⊥c时,b∥c不一定成立,即充分性不成立,
若b∥c,则a⊥c成立,即必要性成立,
则“a⊥c”是“b∥c”的必要不充分条件,
故选:B
点评 本题主要考查充分条件和必要条件的判断,结合直线平行的性质是解决本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
15.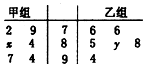 如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩(单位:分),已知甲组数据的众数为84,乙组数据的平均数即为甲组数据的中位数,则x,y的值分别为( )
如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩(单位:分),已知甲组数据的众数为84,乙组数据的平均数即为甲组数据的中位数,则x,y的值分别为( )
 如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩(单位:分),已知甲组数据的众数为84,乙组数据的平均数即为甲组数据的中位数,则x,y的值分别为( )
如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩(单位:分),已知甲组数据的众数为84,乙组数据的平均数即为甲组数据的中位数,则x,y的值分别为( )| A. | 4,5 | B. | 5,4 | C. | 4,4 | D. | 5,5 |
12.已知A(-3,0),B(0,4),点P为直线y=x上一点,过A,B,P三点的圆记作圆C,则“点P为原点”是“圆C的半径取得最小值”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
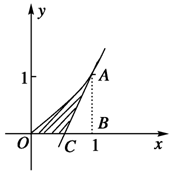 在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围成的面积为$\frac{1}{12}$,试求:
在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围成的面积为$\frac{1}{12}$,试求: