题目内容
20.已知数列{an}是各项均不为零的等差数列,Sn为其前n项和,且${a_n}=\sqrt{{S_{2n-1}}}({n∈{N^*}})$.若不等式$\frac{λ}{{{a_{n+1}}}}≤\frac{n+8}{n}$对任意n∈N*恒成立,则实数λ的最大值为25.分析 推导出an=1+(n-1)×2=2n-1,不等式$\frac{λ}{{{a_{n+1}}}}≤\frac{n+8}{n}$对任意n∈N*恒成立,等价于$\frac{λ}{2(n+1)-1}$$≤\frac{n+8}{n}$对任意n∈N*恒成立,由此利用均值定理能求出实数λ的最大值.
解答 解:∵数列{an}是各项均不为零的等差数列,Sn为其前n项和,且${a_n}=\sqrt{{S_{2n-1}}}({n∈{N^*}})$.
∴${{a}_{n}}^{2}={S}_{2n-1}$,
∴${{a}_{1}}^{2}={S}_{1}={a}_{1}$,由a1>0,解得a1=1,
${{a}_{2}}^{2}={S}_{3}={a}_{1}+{a}_{2}+{a}_{3}$=3a2,由a2>0,解得a2=3,
∴公差d=a2-a1=2,
an=1+(n-1)×2=2n-1.
∵不等式$\frac{λ}{{{a_{n+1}}}}≤\frac{n+8}{n}$对任意n∈N*恒成立,
∴$\frac{λ}{2(n+1)-1}$$≤\frac{n+8}{n}$对任意n∈N*恒成立,
∴$λ≤\frac{n+8}{n}×(2n+1)$=$\frac{2{n}^{2}+17n+8}{n}$=$2n+\frac{8}{n}+17$≥2$\sqrt{2n×\frac{8}{n}}$+17=25.
当且仅当2n=$\frac{8}{n}$,即n=2时,取等号,
∴实数λ的最大值为25.
故答案为:25.
点评 本题考查实数的最大值的求法,是中档题,解题时要认真审题,注意等差数列的性质和均值定理的合理运用.

练习册系列答案
相关题目
8.设集合U=R,集合$A=\left\{{x\left|{{{log}_2}x<1}\right.}\right\},B=\left\{{x\left|{{x^2}-2x-3≤0}\right.}\right\}$,则(∁UA)∩B=( )
| A. | [2,3] | B. | [-1,2] | C. | [-1,0] | D. | [-1,0]∪[2,3] |
15.对任意实数a,b,定义运算“⊕”:$a⊕b=\left\{\begin{array}{l}b,a-b≥1\\ a,a-b<1\end{array}\right.$,设f(x)=(x2-1)⊕(4+x),若函数y=f(x)-k有三个不同零点,则实数k的取值范围是( )
| A. | (-1,2] | B. | [0,1] | C. | [-1,3) | D. | [-1,1) |
12.在△ABC中,a,b,c分别是A,B,C的对边,$a=2\sqrt{3},b=2\sqrt{2}$,且1+2cos(B+C)=0,则BC边上的高等于( )
| A. | $2({\sqrt{3}+1})$ | B. | $2({\sqrt{3}-1})$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
9.在△ABC中,角A,B,C所对的边分别为a,b,c,若A,B,C成等差数列,2a,2b,2c成等比数列,则sinAcosBsinC=( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{\sqrt{3}}{8}$ |
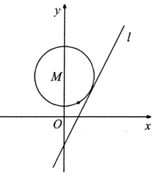 已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).
已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).