题目内容
数列{an}的前n项和记为Sn,a1=1,an+1=4Sn+1(n∈N+).
(1)求a2,a3;
(2)求数列{an}的通项公式.
(1)求a2,a3;
(2)求数列{an}的通项公式.
考点:数列递推式,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)利用已知条件通过n=1,2即可求出a2,a3;
(2)转化已知条件,推出数列是等比数列,即可求解数列的通项公式.
(2)转化已知条件,推出数列是等比数列,即可求解数列的通项公式.
解答:
解:(1)a2=4a1+1=5,
a3=4(a1+a2)+1=25.4分
(2)由an+1=4Sn+1,得an=4Sn-1+1(n≥2),
两式相减,得an+1=5an(n≥2).
又a2=5=5a1,所以
=5,
所以数列{an}是以a1=1为首项,5为公比的等比数列,
所以an=5n-1.10分.
a3=4(a1+a2)+1=25.4分
(2)由an+1=4Sn+1,得an=4Sn-1+1(n≥2),
两式相减,得an+1=5an(n≥2).
又a2=5=5a1,所以
| an+1 |
| an |
所以数列{an}是以a1=1为首项,5为公比的等比数列,
所以an=5n-1.10分.
点评:本题考查递推关系式的应用,数列的通项公式的求法,考查计算能力.

练习册系列答案
相关题目
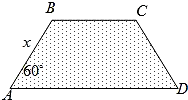 某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9
某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9| 3 |
| 3 |
| A、[3,5] |
| B、(3,5) |
| C、(2,6] |
| D、[2,6) |




