题目内容
已知下列四个命题;
①函数g(x)=1+
是奇函数;
②函数f(x)=log2x满足:对于任意x1,x2∈R,且x1≠x2,都有f(
)>
[f(x1)+f(x2)];
③若函数f(x)满足f(x-1)=-f(x+1),f(1)=2,则f(7)=-2;
④设x1,x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根,则x1x2=1;
其中正确的命题的序号是 .
①函数g(x)=1+
| 2 |
| 2x-1 |
②函数f(x)=log2x满足:对于任意x1,x2∈R,且x1≠x2,都有f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
③若函数f(x)满足f(x-1)=-f(x+1),f(1)=2,则f(7)=-2;
④设x1,x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根,则x1x2=1;
其中正确的命题的序号是
考点:命题的真假判断与应用
专题:综合题,函数的性质及应用
分析:①利用g(-x)+g(x)=0可判断其奇偶性;
②作出f(x)=log2x的图象,数形结合即可判断②的正误;
③易知f(x)是以4为周期的函数,结合题意可求得f(7)=-2;
④x1,x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根⇒logax1=-logax2,进一步整理可得x1x2=1,从而可知④的正误.
②作出f(x)=log2x的图象,数形结合即可判断②的正误;
③易知f(x)是以4为周期的函数,结合题意可求得f(7)=-2;
④x1,x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根⇒logax1=-logax2,进一步整理可得x1x2=1,从而可知④的正误.
解答:
解:①,∵g(-x)+g(x)
=(1+
)+(1+
)
=2+
+
=
+
+2
=-2+
+
+2
=0,
∴g(-x)=-g(x),即①正确;
②,作出f(x)=log2x的图象,
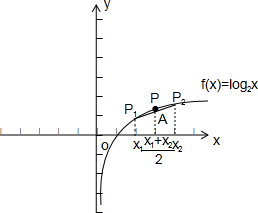
由图知,曲线上点P(其横坐标为
)的纵坐标大于线段P1P2的中点A的纵坐标,即f(
)>
[f(x1)+f(x2)],②正确;
③,∵f(x-1)=-f(x+1),令t=x-1,
则f(t+2)=-f(t),即f(t+4)=f(t),
∴f(x+4)=f(x),
∴f(x)是以4为周期的函数,又f(1)=2,f(x-1)=-f(x+1),
∴f(7)=f(3)=-f(2-1)=-f(1)=-2,即③正确;
④,∵x1,x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根,
∴logax1=-logax2=loga
,
∴x1=
,即x1x2=1,故④正确;
综上所述,正确的命题的序号是①②③④,
故答案为:①②③④.
=(1+
| 2 |
| 2-x-1 |
| 2 |
| 2x-1 |
=2+
| 2•2x |
| 1-2x |
| 2 |
| 2x-1 |
=
| 2(2x-1)+2 |
| 1-2x |
| 2 |
| 2x-1 |
=-2+
| 2 |
| 1-2x |
| 2 |
| 2x-1 |
=0,
∴g(-x)=-g(x),即①正确;
②,作出f(x)=log2x的图象,
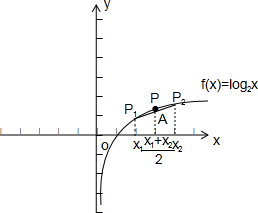
由图知,曲线上点P(其横坐标为
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
③,∵f(x-1)=-f(x+1),令t=x-1,
则f(t+2)=-f(t),即f(t+4)=f(t),
∴f(x+4)=f(x),
∴f(x)是以4为周期的函数,又f(1)=2,f(x-1)=-f(x+1),
∴f(7)=f(3)=-f(2-1)=-f(1)=-2,即③正确;
④,∵x1,x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根,
∴logax1=-logax2=loga
| 1 |
| x2 |
∴x1=
| 1 |
| x2 |
综上所述,正确的命题的序号是①②③④,
故答案为:①②③④.
点评:本题考查命题的真假判断与应用,着重考查函数的奇偶性、单调性、周期性及函数图象的应用,考查分析与应用能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合S={0,a},T={x∈Z|x2<2},则“a=1”是“S⊆T”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
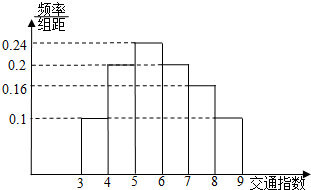
 下列是容量为100的样本的频率分布直方图,则样本数据落在范围〔6,10〕内的频数值为
下列是容量为100的样本的频率分布直方图,则样本数据落在范围〔6,10〕内的频数值为