题目内容
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念性指数值,交通指数取值范围为0~10,分为五个级别,0~2 畅 通;2~4 基本畅通;4~6 轻度拥堵;6~8 中度拥堵;8~10 严重拥堵.早高峰时段,从昆明市交通指挥中心随机选取了二环以内的50个交通路段,依据其交通指数数据绘制的直方图如右.
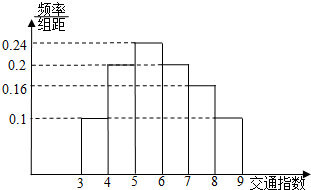
(1)据此估计,早高峰二环以内的三个路段至少有一个是严重拥堵的概率是多少?
(2)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望.

(1)据此估计,早高峰二环以内的三个路段至少有一个是严重拥堵的概率是多少?
(2)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望.
考点:频率分布直方图,离散型随机变量的期望与方差
专题:图表型,概率与统计
分析:(1)由频率分布直方图知“一个路段严重拥堵”的概率为0.1,三个路段“至少一个路段严重拥堵”的对立事件是“三个路段都不严重拥堵”,
求得对立事件的概率,根据事件与其对立事件的概率和为1求三个路段至少有一个是严重拥堵的概率;
(2)根据直方图列出所有时间的分布列,代入期望公式计算.
求得对立事件的概率,根据事件与其对立事件的概率和为1求三个路段至少有一个是严重拥堵的概率;
(2)根据直方图列出所有时间的分布列,代入期望公式计算.
解答:
解:(1)设事件A“一个路段严重拥堵”,则P(A)=0.1,
事件B“至少一个路段严重拥堵”,则P(
)=(1-P(A))3=0.729,
P(B)=1-P(
)=1-0.729=0.271.
∴三个路段至少有一个是严重拥堵的概率是0.271;
(2)分布列如下表:
EX=30×0.1+36×0.44+0.36×42+60×0.1=39.96,
此人经过该路段所用时间的数学期望是39.96分钟.
事件B“至少一个路段严重拥堵”,则P(
. |
| B |
P(B)=1-P(
. |
| B |
∴三个路段至少有一个是严重拥堵的概率是0.271;
(2)分布列如下表:
| X | 30 | 36 | 42 | 60 |
| P | 0.1 | 0.44 | 0.36 | 0.1 |
此人经过该路段所用时间的数学期望是39.96分钟.
点评:本题考查了频率分布直方图及离散型随机变量的分布列与方差,是概率统计的常见题型,本题利用了求对立事件的概率来求事件的概率.

练习册系列答案
相关题目
在平面直角坐标系xOy中,已知
=(-1,t),
=(2,2),若∠ABO=90°,则t=( )
| OA |
| OB |
| A、2 | B、4 | C、5 | D、8 |
直线y-1=k(x-3)被圆(x-2)2+(y-2)2=4所截得的最短弦长等于( )
A、
| ||
B、2
| ||
C、2
| ||
D、
|
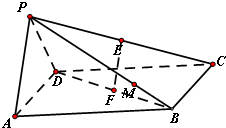 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.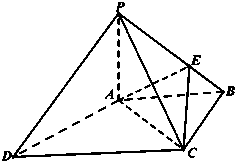 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.