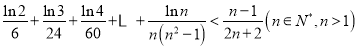Question

【题目】已知函数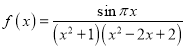.下列命题为真命题的是（ ）

A.函数是周期函数B.函数既有最大值又有最小值

C.函数的定义域是，且其图象有对称轴D.对于任意，单调递减

Answer 1

【答案】BC

【解析】

将函数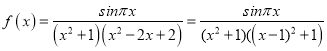，利用对称性判断C,利用函数性质判断AD，利用导数判断C即可．

由函数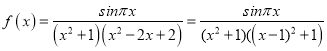

A.函数f（x）是周期函数不正确，因为分母随着自变量的远离原点，趋向于正穷大，所以函数图象无限靠近于x轴，故不是周期函数；

B. 令， 单调递增，又且对称轴是x＝，故在取得最小值，又在取得最大值，故函数有最大值；

另一方面，当恒成立，且因为<0在 恒成立，故的最小值在 取得，由，单增，又 单调递减，同理，在单调递减，在 单调递减，在单增，故

故f（x）有最大值又有最小值；B正确．

C.函数f（x）的定义域是R，且故其对称轴是x＝，此命题正确；

D，f（），f（），∴f（）＜f（），故D不正确，

综上，BC

故选：BC．