题目内容
已知函数f(x)=aex+
x2+bx,曲线y=f(x)在点(0,f(0))处的切线为y-1=0.
(1)求f(x)的解析式及单调区间;
(2)若m为整数,且当x>ln2时,(x-m)(f′(x)-x-1)+2x+1>0,求m的最大值.
| 1 |
| 2 |
(1)求f(x)的解析式及单调区间;
(2)若m为整数,且当x>ln2时,(x-m)(f′(x)-x-1)+2x+1>0,求m的最大值.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求函数的导数,根据导数的几何意义即可求f(x)的解析式及单调区间;
(2)求函数的表达式,姜不等式恒成立转化为求函数的最值问题,解不等式即可得到结论.
(2)求函数的表达式,姜不等式恒成立转化为求函数的最值问题,解不等式即可得到结论.
解答:
解:(1)函数f(x)的导数为f′(x)=aex+x+b,
∵直线y-1=0的斜率为0,且过点(0,1),
∴
,即
,解得a=1,b=-1.
∴f(x)的解析式为f(x)=ex+
x2-x,
∵f′(x)=ex+x-1,
∴当x<0时,f′(x)=ex+x-1<0,此时函数单调递减,
当x>0时,f′(x)=ex+x-1>0,此时函数单调递增,
即函数的增区间为(0,+∞),减区间为(-∞,0).
(2)∵(x-m)(f′(x)-x-1)+2x+1=(x-m)(ex-2)+2x+1,
故当x>ln2时,(x-m)(f′(x)-x-1)+2x+1>0,等价为,m<
+x,(x>ln2),①,
令g(x)=
+x,(x>ln2),
则g′(x)=
+1=
.
令h(x)=ex-2x-3,则h′(x)=ex-2,
∵x>ln2,∴h′(x)=ex-2>0,
即h(x)在(ln2,+∞)上存在唯一的零点,
故g′(x)在(ln2,+∞)上存在唯一的零点,
设此零点为a,则a∈(1,2),
当x∈(ln2,a)时,g′(x)<0,
当x∈(a,+∞)时,g′(x)>0,
故g(x)在(ln2,+∞)上的最小值为g(a),
由g′(a)=0,可得ea=2a+3,
∴g(a)=a+1∈(2,3),
由于①等价于m<g(a),故m的最大值是2.
∵直线y-1=0的斜率为0,且过点(0,1),
∴
|
|
∴f(x)的解析式为f(x)=ex+
| 1 |
| 2 |
∵f′(x)=ex+x-1,
∴当x<0时,f′(x)=ex+x-1<0,此时函数单调递减,
当x>0时,f′(x)=ex+x-1>0,此时函数单调递增,
即函数的增区间为(0,+∞),减区间为(-∞,0).
(2)∵(x-m)(f′(x)-x-1)+2x+1=(x-m)(ex-2)+2x+1,
故当x>ln2时,(x-m)(f′(x)-x-1)+2x+1>0,等价为,m<
| 2x+1 |
| ex-2 |
令g(x)=
| 2x+1 |
| ex-2 |
则g′(x)=
| -2xex+ex-4 |
| (ex-2)2 |
| ex(ex-2x-3) |
| (ex-2)2 |
令h(x)=ex-2x-3,则h′(x)=ex-2,
∵x>ln2,∴h′(x)=ex-2>0,
即h(x)在(ln2,+∞)上存在唯一的零点,
故g′(x)在(ln2,+∞)上存在唯一的零点,
设此零点为a,则a∈(1,2),
当x∈(ln2,a)时,g′(x)<0,
当x∈(a,+∞)时,g′(x)>0,
故g(x)在(ln2,+∞)上的最小值为g(a),
由g′(a)=0,可得ea=2a+3,
∴g(a)=a+1∈(2,3),
由于①等价于m<g(a),故m的最大值是2.
点评:本题主要考查函数单调性的判断,根据函数单调性和导数之间的关系,进行求导是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在等差数列{an}中,若a1+a13=12,则a7为( )
| A、6 | B、7 | C、8 | D、9 |
甲乙丙三位同学独立的解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为
、
、
,则有人能够解决这个问题的概率为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
平面向量
与
的夹角为60°,
=(1,0),|
|=1,则
•(
-3
)等于( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
| D、1 |
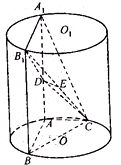 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.