��Ŀ����
��������y2=4x�Ľ�������Բ���ҽ����غϣ���Բ������ϰ��ύ�ڵ�B2��������Ұ��ύ�ڵ�A2����Բ�����ҽ���ΪF1��F2����3|
|cos��B2F1F2=
|
|
��1������Բ�ı����̣�
��2������D��0��2����ֱ�ߣ�б��Ϊk��k��0��������Բ����M��N���㣮
��i����M��N���е�ΪH���Ҵ��ڷ���ʵ����ʹ��
=��
�����б��k��ֵ��
��ii���������Ƿ���ڵ�Q��m��0����ʹ����QM��QNΪ�ڱߵ��ı����Ǹ����Σ����������m�ķ�Χ���������ڣ���˵�����ɣ�
| F1B2 |
| 3 |
| OB2 |
��1������Բ�ı����̣�
��2������D��0��2����ֱ�ߣ�б��Ϊk��k��0��������Բ����M��N���㣮
��i����M��N���е�ΪH���Ҵ��ڷ���ʵ����ʹ��
| OH |
| A2B2 |
��ii���������Ƿ���ڵ�Q��m��0����ʹ����QM��QNΪ�ڱߵ��ı����Ǹ����Σ����������m�ķ�Χ���������ڣ���˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺Բ�����е���ֵ�뷶Χ����
��������1������֪��������Բ�Ľ���F1��-1��0����F2��1��0����b=
c=
���ɴ��������Բ�ı����̣�
��2����������ֱ�ߵķ���Ϊy=kx+2��k��0��������Բ����M��x1��y1����N��x2��y2�����㣬��
���ã�4k2+3��x2+16kx+4=0���ɴ����ø����б�ʽ���е����깫ʽ��Τ�ﶨ���������֪���������б��k��ֵ��
��3���������ϴ��ڵ�Q��m��0����ʹ����QM��QNΪ�ڱߵ��ı����Ǹ�������kHQ•kMN=-1����m=-
=-
��-
���ɴ������m�ķ�Χ��
| 3 |
| 3 |
��2����������ֱ�ߵķ���Ϊy=kx+2��k��0��������Բ����M��x1��y1����N��x2��y2�����㣬��
|
��3���������ϴ��ڵ�Q��m��0����ʹ����QM��QNΪ�ڱߵ��ı����Ǹ�������kHQ•kMN=-1����m=-
| 2k |
| 4k2+3 |
| 2 | ||
4k+
|
| ||
| 6 |
���
�⣺��1��������y2=4x�Ľ���Ϊ��1��0����
����Բ�Ľ���F1��-1��0����F2��1��0����
��̰��᳤b�������᳤a��
��|
|cos��B2F1F2=
|
|��
��b=
c=
��a=2��
����Բ�ı�����Ϊ
+
=1��
��2����������ֱ�ߵķ���Ϊy=kx+2��k��0��
������Բ����M��x1��y1����N��x2��y2�����㣬
��
���ã�4k2+3��x2+16kx+4=0��
��=12k2-3��0����k��0�����k��
��
x1+x2=
��x1x2=
��
MN���е�H��
��
����
��
��
��
kOH=
=kA1B1=
=-
��
���k=
��
����k=
��
��3���������ϴ��ڵ�Q��m��0����ʹ����QM��QNΪ�ڱߵ��ı����Ǹ����Σ�
��HQ��MN��kHQ•kMN=-1��
•k=-1��
��k��
����m=-
=-
��-
=-
��
���ҽ���4k=
��k��
����k=
ʱ��ȡ�Ⱥţ�
��m=-
��0��
�������ϴ��ڵ�Q��m��0����ʹ����QM��QNΪ�ڱߵ��ı����Ǹ����Σ�
m�ķ�Χ��[-
��0����
����Բ�Ľ���F1��-1��0����F2��1��0����
��̰��᳤b�������᳤a��
��|
| F2B2 |
| ||
| 3 |
| OB2 |
��b=
| 3 |
| 3 |
����Բ�ı�����Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��2����������ֱ�ߵķ���Ϊy=kx+2��k��0��
������Բ����M��x1��y1����N��x2��y2�����㣬
��
|
��=12k2-3��0����k��0�����k��
| 1 |
| 2 |
x1+x2=
| -16k |
| 4k2+3 |
| 4 |
| 4k2+3 |
MN���е�H��
| -8k |
| 4k2+3 |
| 6 |
| 4k2+3 |
��
| OH |
| A2B2 |
kOH=
| ||
|
| ||
| 0-2 |
| ||
| 2 |
���k=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
��3���������ϴ��ڵ�Q��m��0����ʹ����QM��QNΪ�ڱߵ��ı����Ǹ����Σ�
��HQ��MN��kHQ•kMN=-1��
| ||
|
��k��
| 1 |
| 2 |
| 2k |
| 4k2+3 |
| 2 | ||
4k+
|
| 2 | ||||
2
|
| ||
| 6 |
���ҽ���4k=
| 3 |
| k |
| 1 |
| 2 |
| ||
| 2 |
��m=-
| 2k |
| 4k2+3 |
�������ϴ��ڵ�Q��m��0����ʹ����QM��QNΪ�ڱߵ��ı����Ǹ����Σ�
m�ķ�Χ��[-
| ||
| 6 |
���������⿼����Բ�ı����̵�������б��k��ֵ��������ʵ����ȡֵ��Χ��������ʱҪ�������⣬ע�⺯���뷽��˼��ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
������y2=
x�Ľ��������ǣ�������
| 1 |
| 4 |
| A����1��0�� | ||
B����
| ||
| C����0��1�� | ||
D����0��
|


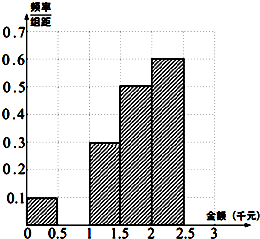 ij�������о�����Ϊ��ͳ��ij�������꣨18�����£�2014�괺������ѹ��Ǯ����������о������������ȥ���������˸���60������������ѹ��Ǯ��������õ���������ͳ�Ʊ���
ij�������о�����Ϊ��ͳ��ij�������꣨18�����£�2014�괺������ѹ��Ǯ����������о������������ȥ���������˸���60������������ѹ��Ǯ��������õ���������ͳ�Ʊ���