Question

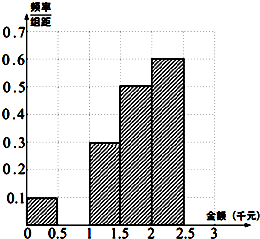某青少年研究中心为了统计某市青少年（18岁以下）2014年春节所收压岁钱的情况进而研究青少年的消费去向，随机抽查了该市60名青少年所收压岁钱的情况，得到如下数据统计表：

压岁钱（单位：千元）	频数	频率
（0，0.5]	3	0.05
（0.5，1]	x	p
（1，1.5]	9	0.15
（1.5，2]	15	0.25
（2，2.5]	18	0.30
（2.5，3]	y	q
合计	60	1.00

已知“超过2千元的青少年”与“不超过2千元的青少年”人数比恰好为2：3．
（Ⅰ）试确定x，y，p，q的值，并补全频率分布直方图（如图）．
（Ⅱ）该机构为了进一步了解这60名青少年压岁钱的消费去向，从“超过2千元的青少年”、“不超过2千元的青少年”中用分层抽样的方法确定10人，若需从这10人中随机选取3人进行问卷调查．设为选取的3人中“超过2千元的青少年”的人数，求的分布列和数学期望．
（Ⅲ）若以频率估计概率，从该市青少年中随机抽取15人进行座谈，若15人中“超过2千元的青少年”的人数为η，求η的期望．

Answer 1

考点：离散型随机变量的期望与方差,分层抽样方法

专题：概率与统计

分析：（Ⅰ）根据题意，有

3+x+9+15+18+y=60 18+y 3+x+9+15 = 2 3

，由此能确定x，y，p，q的值，并补全频率分布直方图．（Ⅱ）用分层抽样的方法，从中选取10人，其中“超过2千元的青少年”有4人，“不超过2千元的青少年”有6人，ξ的可能取值为0，1，2，3，分别求出相应的概率，由此能示出ξ的分布列和Eξ．
（Ⅲ）以频率估计概率，从该市青少年中随机抽取1人为“超过2千元的青少年”的概率为

2

5

，由η～B（15，

2

5

），能求出随机变量η的期望．

解答： 解：（Ⅰ）根据题意，有：

3+x+9+15+18+y=60 18+y 3+x+9+15 = 2 3

，
解得x=9，y=6，
∴p=0.15，q=0.10．
补全频率分布直方图如图所示．
（Ⅱ）用分层抽样的方法，从中选取10人，
则其中“超过2千元的青少年”有10×

2

5

=4人，
“不超过2千元的青少年”有10×

3

5

=6人，
∴ξ的可能取值为0，1，2，3，
P（ξ=0）=

C 0 4 C 3 6

C 3 10

=

1

6

，
P（ξ=1）=

C 1 4 C 2 6

C 3 10

=

1

2

，
P（ξ=2）=

C 2 4 C 1 6

C 3 10

=

3

10

，
P（ξ=3）=

C 3 4 C 0 6

C 3 10

=

1

30

，
∴ξ的分布列为：

ξ	0	1	2	3
p	1 6	1 2	3 10	1 30

Eξ=0×

1

6

+1×

1

2

+2×

3

10

+3×

1

30

=

6

5

．
（Ⅲ）以频率估计概率，
从该市青少年中随机抽取1人为“超过2千元的青少年”的概率为

2

5

，
则η～B（15，

2

5

），
∴随机变量η的期望为Eη=15×

2

5

=6．

点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，是中档题．