题目内容
抛物线y2=
x的焦点坐标是（ ）
| 1 |
| 4 |
| A、（1，0） | ||
B、（
| ||
| C、（0，1） | ||
D、（0，
|
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据抛物线的标准方程，求出p值，确定开口方向，从而写出焦点坐标．
解答：
解：抛物线y2=
x，开口向右，p=
，
故焦点坐标为 （
，0），
故选：B．
| 1 |
| 4 |
| 1 |
| 8 |
故焦点坐标为 （
| 1 |
| 16 |
故选：B．
点评：本题考查抛物线的标准方程，以及简单性质的应用，属于容易题．
练习册系列答案
相关题目
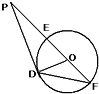如图，已知P是⊙O外一点，PD为⊙O的切线，D为切点，割线PEF经过圆心O．若PF=16，PD=4| 3 |
| A、13 | B、6.5 | C、7 | D、8 |
若a＞b，则下列不等式一定成立的是（ ）
| A、2a＞2b | ||||
| B、a2＞b2 | ||||
| C、ac＞bc | ||||
D、
|
直线l1：（2-a）x+ay+3=0和直线l2：x-ay-3=0，若直线l1的法向量恰好是直线l2的方向向量，则实数a的值为（ ）
| A、-2 | B、1 | C、-2或1 | D、0 |
复数
的共轭复数在复平面内对应的点位于（ ）
| 1+i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
一元二次不等式（x-1）（x-3）＜0的解集是（ ）
| A、（-∞，1） |
| B、（1，3） |
| C、（3，+∞） |
| D、（-∞，1）∪（3，+∞） |