题目内容
10．在极坐标系中，过点A（1，π）且垂直于极轴的直线的极坐标方程为（ ）| A． | ρ=sinθ | B． | ρ=1 | C． | ρcosθ=-1 | D． | ρsinθ=-1 |
分析 先求出点P的直角坐标为（-1，0），从而求出l的直角坐标方程是x=-1，由此能求出直线l的极坐标方程．
解答 解：∵在极坐标系中，点A（1，π），
∴点P的直角坐标为（-1，0），
∴l的直角坐标方程是x=-1，
化为极坐标方程化为 ρcosθ=-1，
故选：C．
点评 本题考查直线的极坐标方程的求法，考查直角坐标方程、极坐标方程、参数方程的互化等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想，是中档题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
20．定义在R上的函数f（x）满足：①f（-x）=-f（x）；②f（2x）=af（x）（a＞0）；③当2≤x≤4时，$f（x）=|sin\frac{π}{2}x|$，若分别以函数f（x）的极值点和相应极值为横、纵坐标的点都在一条直线上，则a的值为（ ）
| A． | 1 | B． | 2 | C． | 1或2 | D． | 2或3 |
1．网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（ ）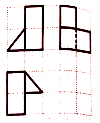
| A． | 2 | B． | 4 | C． | $\frac{2\sqrt{2}}{3}$ | D． | 1+$\frac{2\sqrt{2}}{3}$ |
5．执行如图的程序框图，输出S的值是（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | -1 |
2．已知a，b，c∈R，则下列推证中正确的是（ ）
| A． | a＞b⇒am2＞bm2 | B． | $\frac{a}{c}＞\frac{b}{c}$⇒a＞b | ||
| C． | ac2＞bc2⇒a＞b | D． | a2＞b2，ab＞0⇒$\frac{1}{a}＜\frac{1}{b}$ |