题目内容
已知F1,F2是双曲线
-
=1(a>0,b>0)的左右焦点,点P在双曲线上不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A,若|OA|=b,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题设条件推导出PQ=PF2,由双曲线性质推导出PF1-PQ=QF1=2a,由中位线定理推导出QF1=2a=2OA=2,由此及彼能求出双曲线的离心率.
解答:
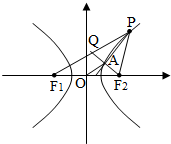 解:∵F1,F2是双曲线
解:∵F1,F2是双曲线
-
=1(a>0,b>0)的左右焦点,
延长F2A交PF1于Q,
∵PA是∠F1PF2的角平分线,∴PQ=PF2,
∵P在双曲线上,∴PF1-PF2=2a,
∴PF1-PQ=QF1=2b,
∵O是F1F2中点,A是F2Q中点,
∴OA是F2F1Q的中位线,∴QF1=2a=2OA=2,
∴a=1,c=
,
∴双曲线的离心率e=
.
故答案为:
.
 解:∵F1,F2是双曲线
解:∵F1,F2是双曲线| x2 |
| a2 |
| y2 |
| b2 |
延长F2A交PF1于Q,
∵PA是∠F1PF2的角平分线,∴PQ=PF2,
∵P在双曲线上,∴PF1-PF2=2a,
∴PF1-PQ=QF1=2b,
∵O是F1F2中点,A是F2Q中点,
∴OA是F2F1Q的中位线,∴QF1=2a=2OA=2,
∴a=1,c=
| 2 |
∴双曲线的离心率e=
| 2 |
故答案为:
| 2 |
点评:本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,要熟练掌握双曲线的性质.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
若变量x,y满足约束条件
,则目标函数z=3x-y的最小值为( )
|
| A、-4 | ||
| B、0 | ||
C、
| ||
| D、4 |
(1-2x)5的展开式中x2的系数是( )
| A、10 | B、-10 |
| C、40 | D、-40 |
 已知椭圆C的方程为
已知椭圆C的方程为 已知曲线C1:
已知曲线C1: