题目内容
9.直角三角形ABC中,A=90°,B=60°,B,C为双曲线E的两个焦点,点A在双曲线E上,则该双曲线的离心率为( )| A. | $\sqrt{3}+1$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 根据直角三角形的边角关系,以及双曲线的定义和性质,建立方程关系求出a,c的关系进行求解即可.
解答 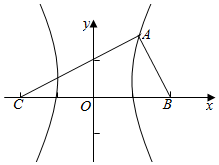 解:不妨设双曲线方程为$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0),
解:不妨设双曲线方程为$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0),
设A在双曲线右支上,
∵A=90°,B=60°,
∴C=30°,
则BC=2c,则AB=$\frac{1}{2}$BC=c,
则AC=$\sqrt{3}$c,
∵AC-AB=2a,
∴$\sqrt{3}$c-c=2a,即($\sqrt{3}$-1)c=2a,
即e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}-1}$=$\frac{2(\sqrt{3}+1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}+1)}{2}$=$\sqrt{3}+1$,
故选:A
点评 本题主要考查双曲线离心率的计算,根据双曲线的性质,结合三角形的边角关系建立方程关系是解决本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
19.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$以及双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的渐近线将第一象限三等分,则双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的离心率为( )
| A. | 2或$\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{6}$或$\frac{{2\sqrt{3}}}{3}$ | C. | 2或$\sqrt{3}$ | D. | $\sqrt{3}$或$\sqrt{6}$ |
20.不等式$\frac{1+x}{1-x}$≥0的解集为( )
| A. | {x|x≥1或≤-1} | B. | {x|-1≤x≤1} | C. | {x|x≥1或x<-1} | D. | {x|-1≤x<1} |
18.已知点A为双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)上任意一点,且它到双曲线的两条渐近线的距离之积为定值3,则$\frac{1}{a^2}$+$\frac{1}{b^2}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |