题目内容
17.在边长为1的等边△ABC中,P为直线BC上一点,若$\overrightarrow{AP}=(2-λ)\overrightarrow{AB}+2λ\overrightarrow{AC},λ∈R$,则λ=-1,$\overrightarrow{AP}•\overrightarrow{AC}$=$-\frac{1}{2}$.分析 由P为直线BC上一点便可得出$\overrightarrow{AP}=(1-k)\overrightarrow{AB}+k\overrightarrow{AC}$,这样由平面向量基本定理即可得出2-λ+2λ=1,求出λ=-1,从而得出$\overrightarrow{AP}•\overrightarrow{AC}=(3\overrightarrow{AB}-2\overrightarrow{AC})•\overrightarrow{AC}$,根据条件进行数量积的运算便可求出$\overrightarrow{AP}•\overrightarrow{AC}$的值.
解答  解:如图,
解:如图,
P为直线BC上一点;
∴设$\overrightarrow{BP}=k\overrightarrow{BC}$;
∴$\overrightarrow{AP}-\overrightarrow{AB}=k(\overrightarrow{AC}-\overrightarrow{AB})$;
∴$\overrightarrow{AP}=(1-k)\overrightarrow{AB}+k\overrightarrow{AC}$;
又$\overrightarrow{AP}=(2-λ)\overrightarrow{AB}+2λ\overrightarrow{AC}$;
∴2-λ+2λ=1;
∴λ=-1;
∴$\overrightarrow{AP}=3\overrightarrow{AB}-2\overrightarrow{AC}$;
∴$\overrightarrow{AP}•\overrightarrow{AC}=(3\overrightarrow{AB}-2\overrightarrow{AC})•\overrightarrow{AC}$
=$3\overrightarrow{AB}•\overrightarrow{AC}-2{\overrightarrow{AC}}^{2}$
=$3×1×1×\frac{1}{2}-2×{1}^{2}$
=$-\frac{1}{2}$.
故答案为:-1,-$\frac{1}{2}$.
点评 考查共线向量基本定理,平面向量基本定理,向量的数乘运算,以及向量数量积的运算及计算公式.

 阅读快车系列答案
阅读快车系列答案| A. | {x|2<x<3} | B. | {x|1<x<3} | C. | {x|1<x<2} | D. | {x|x>1} |
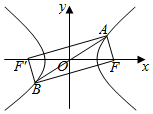 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )| A. | $[{\sqrt{2},\sqrt{3}+1}]$ | B. | $[{\sqrt{3},2+\sqrt{3}}]$ | C. | $[{\sqrt{2},2+\sqrt{3}}]$ | D. | $[{\sqrt{3},\sqrt{3}+1}]$ |
| A. | $\sqrt{3}+1$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | $\sqrt{7}$ | B. | $\sqrt{6}$ | C. | $\sqrt{3}$ | D. | 7 |
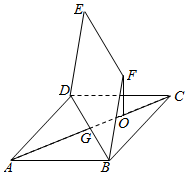 如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.