��Ŀ����
11���趯��M������ԭ��O�ľ��������ֱ�ߵ�l��x=-m��m��0������֮����һ�������ˣ��ǵ�Ĺ켣Ϊ����C����1��������C�ķ��̣�������C����״���ֵ�Ĺ�ϵ��
��2������=$\frac{{\sqrt{2}}}{2}$��m=1ʱ���õ�������ΪC1��������C1����ƽ��һ����λ�õ�����E������P��-2��0����ֱ��l1������E���ڲ�ͬ������A��x1��y1����B��x2��y2������F��1��0����ֱ��AF��BF�ֱ�����E��D��Q����$\overrightarrow{AF}=��\overrightarrow{FD}��\overrightarrow{BF}=��\overrightarrow{FQ}$�������¡�R�����+�µ�ȡֵ��Χ��
���� ��1����M��x��y�����������У�$\sqrt{{x^2}+{y^2}}=��|{x+m}|$��������C�ķ���Ϊ����1-��2��x2+y2-2m��2x-m2��2=0���������ۣ����ɵó����ۣ�
��2���������ۣ�ȷ����=3-2x1����=3-2x2⇒��+��=6-2��x1+x2������l1��y=k��x+2������$\left\{{\begin{array}{l}{y=k��x+2��}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$����ȥy�����ã���2k2+1��x2+8k2x+8k2-2=0������Τ�ﶨ�������ɵó����ۣ�
��� �⣺��1����M��x��y�����������У�$\sqrt{{x^2}+{y^2}}=��|{x+m}|$
������C�ķ���Ϊ����1-��2��x2+y2-2m��2x-m2��2=0
��i����=1ʱ������C�ķ���Ϊ��y2=2m��x+m���������ߣ�
��ii���ˡ�1ʱ������C�ķ���Ϊ��$\frac{{{{��x-\frac{{m{��^2}}}{{1-{��^2}}}��}^2}}}{{\frac{{{m^2}{��^2}}}{{{{��1-{��^2}��}^2}}}}}+\frac{y^2}{{\frac{{{m^2}{��^2}}}{{1-{��^2}}}}}=1$�ˣ�1ʱ������C�ķ���Ϊ������x���ϵ�˫���ߣ� 0���ˣ�1ʱ������C�ķ���Ϊ������x���ϵ���Բ��
��2����$��=\frac{{\sqrt{2}}}{2}��m=1$ʱ������C1�ķ���Ϊ��$\frac{{{{��x-1��}^2}}}{2}+{y^2}=1$��������E�ķ���Ϊ��$\frac{x^2}{2}+{y^2}=1$��
��D��x3��y3������$\overrightarrow{AF}=��1-{x_1}��-{y_1}����\overrightarrow{FD}=��{x_3}-1��{y_3}��$����$\overrightarrow{AF}=��\overrightarrow{FD}$����-y1=��y3����$��=-\frac{y_1}{y_3}$��
��i��AD��x���ֱʱ��AD����Ϊ��$y=\frac{y_1}{{{x_1}-1}}��x-1��$�� $\left\{{\begin{array}{l}{y=\frac{y_1}{{{x_1}-1}}��x-1��}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$����ȥx�������ã�$��3-2{x_1}��{y^2}+2{y_1}��{x_1}-1��y-y_1^2=0$��
�ɸ���ϵ���Ĺ�ϵ�У�${y_1}{y_3}=-\frac{y_1^2}{{3-2{x_1}}}⇒-\frac{y_1}{y_3}=3-2{x_1}⇒��=3-2{x_1}$��
��ii��AD��x�ᴹֱʱ��x1=1����=1Ҳ���㣺��=3-2x1��
ͬ����֤����=3-2x2⇒��+��=6-2��x1+x2��
��l1��y=k��x+2������$\left\{{\begin{array}{l}{y=k��x+2��}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$����ȥy�����ã���2k2+1��x2+8k2x+8k2-2=0��
��������k��0�ҡ�=��8k2��-24��2k2+1����8k2-2����0����0��k2��$\frac{1}{2}$��${x_1}+{x_2}=-\frac{{8{k^2}}}{{2{k^2}+1}}⇒��+��=6+\frac{{16{k^2}}}{{2{k^2}+1}}=14-\frac{8}{{2{k^2}+1}}$��$0��{k^2}��\frac{1}{2}⇒1��2{k^2}+1��2$��
���+�¡ʣ�6��10�����ʦ�+�µ�ȡֵ��ΧΪ��6��10����
���� ���⿼�������뷽�̣�����ֱ������Բλ�ù�ϵ�����ã�����Τ�ﶨ��������������۵���ѧ˼�룬�����е��⣮

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�| A�� | $\frac{\sqrt{3}}{3}$ | B�� | 1 | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\sqrt{3}$ |
| A�� | 5 | B�� | 10 | C�� | 2$\sqrt{6}$ | D�� | 4$\sqrt{6}$ |
| A�� | $\frac{��}{4}$ | B�� | $\frac{��}{6}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{��}{12}$ |
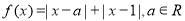 ��
��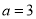 ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ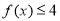 ��
��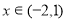 ʱ��
ʱ��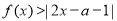 ,��
,��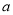 ��ȡֵ��Χ��
��ȡֵ��Χ��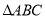 �У�
��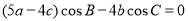 ��
��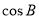 ��ֵ��
��ֵ��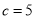 ��b=
��b=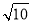 ����
����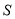 ��
��