题目内容
已知直线x-y+3=0被圆x2+y2+2x-2y+F=0截得的弦长为
,则该圆的标准方程为 .
| 2 |
考点:圆的标准方程
专题:计算题,直线与圆
分析:求出圆心到直线x-y+3=0的距离,利用直线x-y+3=0被圆x2+y2+2x-2y+F=0截得的弦长为
,求出半径,即可求出该圆的标准方程.
| 2 |
解答:
解:圆x2+y2+2x-2y+F=0的圆心为(-1,1),到直线x-y+3=0的距离为
=
,
∵直线x-y+3=0被圆x2+y2+2x-2y+F=0截得的弦长为
,
∴r=
=1
∴圆的标准方程为(x+1)2+(y-1)2=1,
故答案为:(x+1)2+(y-1)2=1.
| |-1-1+3| | ||
|
| ||
| 2 |
∵直线x-y+3=0被圆x2+y2+2x-2y+F=0截得的弦长为
| 2 |
∴r=
(
|
∴圆的标准方程为(x+1)2+(y-1)2=1,
故答案为:(x+1)2+(y-1)2=1.
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,勾股定理,垂径定理,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
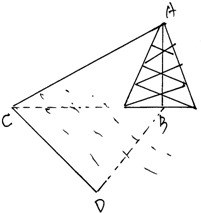 如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=