题目内容
已知公差大于零的等差数列{an}的前n项和为Sn,且满足:a2·a4=65,a1+a5=18.
(1)若1<i<21,a1,ai,a21是某等比数列的连续三项,求i的值;
(2)设bn=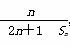 ,是否存在一个最小的常数m使得b1+b2+…+bn<m对于任意的正整数n均成立,若存在,求出常数m;若不存在,请说明理由.
,是否存在一个最小的常数m使得b1+b2+…+bn<m对于任意的正整数n均成立,若存在,求出常数m;若不存在,请说明理由.
解:(1){an}为等差数列,∵a1+a5=a2+a4=18,
又a2·a4=65,∴a2,a4是方程x2-18x+65=0的两个根,
又公差d>0,∴a2<a4,∴a2=5,a4=13.
∴
∴a1=1,d=4.∴an=4n-3.
由1<i<21,a1,ai,a21是某等比数列的连续三项,∴a1·a21=a ,
,
即1·81=(4i-3)2,
解得i=3.
 所以存在m=
所以存在m=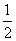 使b1+b2+…+bn<m对于任意的正整数n均成立.
使b1+b2+…+bn<m对于任意的正整数n均成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B.
B.
 D.
D.
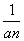 }是等差数列;
}是等差数列;
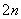 +2an+1,n∈N*.
+2an+1,n∈N*. (其中O为坐标原点),则实数a等于( )
(其中O为坐标原点),则实数a等于( ) 或-
或-