题目内容
18. 如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧AB的中点,设C,D(C在D左侧)为优弧AB上的两个不同的动点,且CD∥BA,记∠POD=α,四边形ABCD的面积为S.
如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧AB的中点,设C,D(C在D左侧)为优弧AB上的两个不同的动点,且CD∥BA,记∠POD=α,四边形ABCD的面积为S.(1)求S关于α的函数关系;
(2)当α为何值时,S取得最大值?并求出S的最大值.
分析 (1)求出O到AB和CD的距离,AB与CD的长,代入梯形面积公式,可得S关于α的函数关系;
(2)结合正弦函数的图象和性质及二次函数的图象和性质,可得S的最大值及最大值点.
解答 解:(1)如下图所示: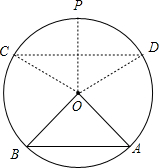
∵圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,
∴AB=$\sqrt{{OB}^{2}+{OA}^{2}}$=2,O到AB的距离d=1,
若∠POD=α,则CD=2$\sqrt{2}$sinα,O到CD的距离h=$\sqrt{2}$cosα,
故S=$\frac{1}{2}$(2$\sqrt{2}$sinα+2)($\sqrt{2}$cosα+1)=2sinαcosα+$\sqrt{2}$(sinα+cosα)+1=(sinα+cosα)2+$\sqrt{2}$(sinα+cosα)=2sin2(α+$\frac{π}{4}$)+2sin(α+$\frac{π}{4}$).
(2)令t=sin(α+$\frac{π}{4}$).则S=2t2+2t,t∈[$\frac{\sqrt{2}}{2}$,1],
∵S=2t2+2t的图象是开口朝上,且以直线t=-$\frac{1}{2}$为对称的抛物线,
故当t=1,即α=$\frac{π}{4}$时,S取最大值4.
点评 本题考查的知识点是函数的解析式的求不地,函数的最值及其几何意义,二次函数的图象和性质,正弦函数的图象和性质,难度中档.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
9.“x<4”是“$\sqrt{x}$<2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
6.设a∈Z,且0≤a<13,若512015+a能被13整除,则a=( )
| A. | 0 | B. | 1 | C. | 11 | D. | 12 |
7.下列关于复数的命题,正确的个数是( )
①复数a+bi与c+di的积是实数的充要条件是ad+bc=0
②命题“已知m为实数,若复数z=m+1+(m-1)i为虚数,则m≠1”的逆命题
③对于任意的z1,z2,z3∈C,有(z1•z2)•z3=z1•(z2•z3)
①复数a+bi与c+di的积是实数的充要条件是ad+bc=0
②命题“已知m为实数,若复数z=m+1+(m-1)i为虚数,则m≠1”的逆命题
③对于任意的z1,z2,z3∈C,有(z1•z2)•z3=z1•(z2•z3)
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
8.下列函数中,图象关于点($\frac{π}{3}$,0)对称的是( )
| A. | y=sin(x+$\frac{π}{3}$) | B. | y=cos(x-$\frac{π}{3}$) | C. | y=sin(x+$\frac{π}{6}$) | D. | y=tan(x+$\frac{π}{6}$) |
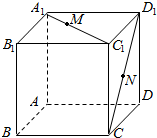 在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=3,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求M,N两点间的距离.
在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=3,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求M,N两点间的距离.