题目内容
设a=
cosxdx,则(2x-
)6展开式的常数项为 .
| ∫ |
0 |
| a |
| x |
考点:二项式系数的性质,定积分
专题:二项式定理
分析:先求定积分,求得a的值,再求出二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项的值.
解答:
解:a=
cosxdx=
sinxdx=1,则(2x-
)6=(2x-
)6,它的展开式通项公式为Tr+1=
•(-1)r•26-r•x6-2r,
令6-2r=0,解得 r=3,
∴(2x-
)6展开式的常数项为-8×
=-160,
故答案为:-160.
| ∫ |
0 |
| ∫ |
0 |
| a |
| x |
| 1 |
| x |
| C | r 6 |
令6-2r=0,解得 r=3,
∴(2x-
| a |
| x |
| C | 3 6 |
故答案为:-160.
点评:本题主要考查求定积分,二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
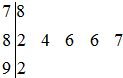 如图是2010年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )
如图是2010年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )| A、4.84 | B、0.8 |
| C、1.6 | D、3.2 |
下列命题中,错误的是( )
| A、过平面α外一点可以作无数条直线与平面α平行 |
| B、与同一个平面所成的角相等的两条直线必平行 |
| C、若直线l垂直平面α内的两条相交直线,则直线l必垂直平面α |
| D、垂直于同一个平面的两条直线平行 |
已知点M(x1,y1)、N(x2,y2)的坐标满足不等式组
,若
=(1,-1),则
•
的取值范围是( )
|
| a |
| MN |
| a |
| A、[-3,3] |
| B、[-4,4] |
| C、[-6,6] |
| D、[-7,7] |
若2m+2n<4,则点(m,n)必在( )
| A、直线x+y-2=0的左下方 |
| B、直线x+y-2=0的右上方 |
| C、直线x+2y-2=0的右上方 |
| D、直线x+2y-2=0的左下方 |
 已知一棱锥的三视图如图所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯形,则该棱锥的体积为
已知一棱锥的三视图如图所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯形,则该棱锥的体积为