题目内容
若非零向量
，
满足|
|=3|
|=|
+2
|，则向量
，
夹角的正弦值为 ．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点：数量积表示两个向量的夹角
专题：三角函数的求值,平面向量及应用
分析：根据题意，利用平面向量的数量积，求出向量
，
夹角的余弦值，再求向量
，
夹角的正弦值．
| a |
| b |
| a |
| b |
解答：
解：∵非零向量
，
满足|
|=3|
|=|
+2
|，
∴
；
即9=9+4×3×1×cos＜
，
＞+4，
∴cos＜
，
＞=-
；
又∵＜
，
＞∈[0，π]，
∴sin＜
，
＞=
=
；
∴向量
，
夹角的正弦值为
．
故答案为：
．
| a |
| b |
| a |
| b |
| a |
| b |
∴
|
即9=9+4×3×1×cos＜
| a |
| b |
∴cos＜
| a |
| b |
| 1 |
| 3 |
又∵＜
| a |
| b |
∴sin＜
| a |
| b |
1-(-
|
2
| ||
| 3 |
∴向量
| a |
| b |
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
点评：本题考查了平面向量的应用问题，也考查了同角的三角函数的应用问题，是基础题目．
练习册系列答案
相关题目
已知定义域为R的函数f（x）满足f（-x）=-f（x+4），且当x＞2时，f（x）单调递增，如果x1+x2＜4，且（x1-2）（x2-2）＜0，则下列说法正确的是（ ）
| A、f（x1）+f（x2）的值为正数 |
| B、f（x1）+f（x2）的值为负数 |
| C、f（x1）+f（x2）的值正负不能确定 |
| D、f（x1）+f（x2）的值一定为零 |
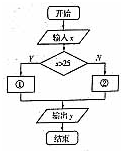某客运部门规定甲、乙两地之间旅客托运行李的费用为：不超过25kg按0.5元/kg收费，超过25kg的部分按0.8元/kg收费，计算收费的程序框图如右图所示，则①②处应填（ ）| A、y=0.8xy=0.5x |
| B、y=0.5xy=0.8x |
| C、y=0.8x-7.5y=0.5x |
| D、y=0.8x+12.5y=0.8x |
一个半径为2的球体经过切割后，剩余部分几何体的三视图如图所示，则该几何体的体积为（ ）A、
| ||
B、
| ||
| C、4π | ||
| D、8π |
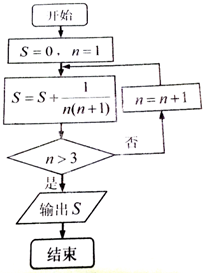
某程序框图如图所示，执行该程序后输出的S的值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如果实数x、y满足条件
，那么z=4x•2-y的最大值为（ ）
|
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|