题目内容
一个半径为2的球体经过切割后，剩余部分几何体的三视图如图所示，则该几何体的体积为（ ）A、
| ||
B、
| ||
| C、4π | ||
| D、8π |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体为一个球切割掉
球体，根据几何体的体积为
球的体积，把数据代入球的体积公式计算可得答案．
| 1 |
| 4 |
| 3 |
| 4 |
解答：
解：由已知中的三视图可得：
几何体为一个球切割掉
球体，
故几何体的体积V=
•
πR3=8π，
故选：D．
几何体为一个球切割掉
| 1 |
| 4 |
故几何体的体积V=
| 3 |
| 4 |
| 4 |
| 3 |
故选：D．
点评：本题考查了由三视图求几何体的表面积和体积，根据三视图判断几何体的形状及数据所对应的几何量是解答此类问题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
对于实数x，符号[x]表示不超过x的最大整数，例如[π]=3，[-1.08]=-2，已知函数f（x）=x-[x]，则下列结论中正确的是（ ）
A、f（sin
| ||||
B、方程f（x）=
| ||||
| C、f（x）是周期函数 | ||||
| D、f（x）是增函数 |
我们把离心率为e=
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
①双曲线x2-
| 2y2 | ||
|
②若b2=ac，则该双曲线是黄金双曲线；
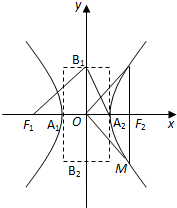
③若∠F1B1A2=90°，则该双曲线是黄金双曲线；
④若∠MON=90°，则该双曲线是黄金双曲线．
| A、①② | B、①③ |
| C、①③④ | D、①②③④ |
执行如图所示的程序框图，如果输入a=2，b=2，那么输出的a值为（ ）
| A、14 | B、15 | C、16 | D、17 |
下列命题中，为真命题的是（ ）
A、?x∈[
| ||
| B、?x∈R，x2＜x3 | ||
C、?x∈(0，
| ||
| D、?x∈R，x2+x=-1 |
设x，y满足约束条件
（ ）
|
| A、6 | ||
B、
| ||
| C、7 | ||
D、
|