题目内容
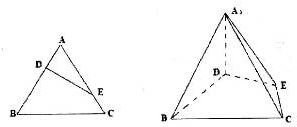 已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足
已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
(1)证明:A1D⊥平面BCDE;
(2)在线段BD上是否存在点M,使得CM∥平面A1DE?若存在,求出BM的长;若不存在,说明理由.
考点:平面与平面垂直的性质,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知条件推导出DE⊥AD,折叠后有DE⊥A1D,由此能证明A1D⊥平面BCDE.
(2)过C作BD边的垂线,垂直即为所求的点M.M为BC边的中点,BM=
.
(2)过C作BD边的垂线,垂直即为所求的点M.M为BC边的中点,BM=
| 3 |
| 2 |
解答:
(1)证明:在△ABC中,
∵
=
=
,等边三角形的边长为3,
∴AD=CE=1,BD=AE=2,
在△ADE中,∠A=60°,AD=1,AE=2,
由余弦定理,得DE=
,
∴AE2=AD2+DE2,
∴△ADE为直角三角形,且DE⊥AD,
折叠后有DE⊥A1D,
∵平面A1DE⊥平面BCDE,
平面A1DE∩平面BCDE=DE,
A1D?平面A1DE,∴A1D⊥平面BCDE.
(2)解:过C作BD边的垂线,垂足即为所求的点M.
证明:由(1)知DE⊥AB于E,于是DE∥CM,
∵CM不包含于平面A1DE,DE?平面A1DE.
∴CM∥平面A1DE,
∵M为BC边的中点,∴BM=
.
∵
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
∴AD=CE=1,BD=AE=2,
在△ADE中,∠A=60°,AD=1,AE=2,
由余弦定理,得DE=
| 3 |
∴AE2=AD2+DE2,
∴△ADE为直角三角形,且DE⊥AD,
折叠后有DE⊥A1D,
∵平面A1DE⊥平面BCDE,
平面A1DE∩平面BCDE=DE,
A1D?平面A1DE,∴A1D⊥平面BCDE.
(2)解:过C作BD边的垂线,垂足即为所求的点M.
证明:由(1)知DE⊥AB于E,于是DE∥CM,
∵CM不包含于平面A1DE,DE?平面A1DE.
∴CM∥平面A1DE,
∵M为BC边的中点,∴BM=
| 3 |
| 2 |
点评:本题考查直线与平面垂直的证明,考查使直线平行于平面的点是否存在的判断与证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
阅读程序(如图),若a=45,b=20,c=10,则输出的结果为( )


| A、10 | B、20 | C、25 | D、45 |
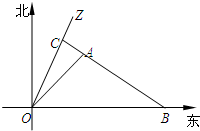 如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口3
如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口3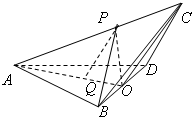 如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且
如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且