题目内容
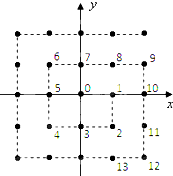 如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,则标签2013×2014的格点的坐标为( )
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,则标签2013×2014的格点的坐标为( )| A、(-1007,1007) |
| B、(1007,1006) |
| C、(-1007,-1007) |
| D、(1006,-1007) |
考点:归纳推理
专题:推理和证明
分析:根据数据,归纳出点(n,-n)处标(2n-1)×2n,即可得到结论.
解答:
解:观察已知中点(1,-1)处标2,即1×2,
点(2,-2)处标12,即3×4,
点(3,-3)处标25,即5×6,
…
由此推断
点(n,-n)处标(2n-1)×2n,
∵2n=2014时,n=1007
故标签2013×2014的格点的坐标为(1007,-1007)
故选:A.
点(2,-2)处标12,即3×4,
点(3,-3)处标25,即5×6,
…
由此推断
点(n,-n)处标(2n-1)×2n,
∵2n=2014时,n=1007
故标签2013×2014的格点的坐标为(1007,-1007)
故选:A.
点评:本题考查数列知识的运用,根据已知平面直角坐标系的格点(横、纵坐标均为整数的点)的规则,找出表上数字标签所示的规律,是解答的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知α∈(0,
),a=(sinα)cosα,b=(sinα)sinα,c=(cosα)sinα,则a、b、c的大小关系是( )
| π |
| 4 |
| A、a>b>c |
| B、c>a>b |
| C、b>a>c |
| D、c>b>a |
若某空间几何体的三视图如图所示,则该几何体的表面积是( )


A、2+
| ||||||
B、2(1+
| ||||||
C、
| ||||||
D、2+
|
在△ABC中,a=2011,b=1,则sinA:sinB等于( )
| A、1:1 | B、1:2011 |
| C、2011:1 | D、不确定 |
点F(c,0)为双曲线
-
=1(a>0,b>0)的右焦点,点P在双曲线上,线段PF与圆(x-
)2+y2=
相切于点Q,且
=2
,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| 3 |
| b2 |
| 9 |
| PQ |
| QF |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
函数y=
在[0,2]上的最大值( )
| x |
| ex |
| A、当x=0时,y=0 | ||||||
B、当x=2时,y=
| ||||||
C、当x=1时,y=
| ||||||
D、当x=
|