题目内容
已知α∈(0,
),a=(sinα)cosα,b=(sinα)sinα,c=(cosα)sinα,则a、b、c的大小关系是( )
| π |
| 4 |
| A、a>b>c |
| B、c>a>b |
| C、b>a>c |
| D、c>b>a |
考点:正弦函数的图象,余弦函数的图象
专题:函数的性质及应用
分析:根据三角函数的图象和性质,求出sinα,cosα的取值范围,利用指数函数和幂函数的单调性即可得到结论.
解答:
解:∵α∈(0,
),
∴sinα∈(0,
),cosα∈(
,1),则sinα<cosα,
则(sinα)cosα<(sinα)sinα,即a<b.
(sinα)sinα<(cosα)sinα,即b<c,
综上c>b>a,
故选:D.
| π |
| 4 |
∴sinα∈(0,
| ||
| 2 |
| ||
| 2 |
则(sinα)cosα<(sinα)sinα,即a<b.
(sinα)sinα<(cosα)sinα,即b<c,
综上c>b>a,
故选:D.
点评:本题主要考查函数值的大小比较,根据指数函数和幂函数的单调性是解决本题的关键.

练习册系列答案
相关题目
定义在R上的函数f(x)满足f(x+6)=f(x),当-3≤x<-1时,f(x)=-(x+2)2;当-1≤x<3时,f(x)=x.则f(1)+f(2)+f(3)+…+f(2013)等于( )
| A、335 | B、337 |
| C、1678 | D、2012 |
(文)已知函数f(x)=f′(
)sinx+cosx,则f(
)的值为( )
| π |
| 6 |
| π |
| 6 |
| A、1 | B、2 | C、-2 | D、-1 |
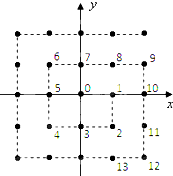 如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,则标签2013×2014的格点的坐标为( )
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,则标签2013×2014的格点的坐标为( )| A、(-1007,1007) |
| B、(1007,1006) |
| C、(-1007,-1007) |
| D、(1006,-1007) |
下列式子正确的是( )
A、
| ||
B、
| ||
C、
| ||
D、(
|
已知向量
、
满足
⊥
,|
|=1,|
|=2
,则|2
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| A、2 | ||
B、2
| ||
| C、4 | ||
| D、16 |