题目内容
已知函数f(x)=cos
x+
,则f(x)在[-4,6]上所有零点的和为 .
| π |
| 2 |
| 1 |
| x-1 |
考点:余弦函数的图象
专题:函数的性质及应用,三角函数的图像与性质
分析:首先:令f(x)=0即:cos
x+
=0则:设y1=cos
x y2=-
在坐标系内画出y1=cos
x 和y2=-
的图象图象有6个交点,其中有三对都关于x=1对称,进一步求出结果.
| π |
| 2 |
| 1 |
| x-1 |
| π |
| 2 |
| 1 |
| x-1 |
| π |
| 2 |
| 1 |
| x-1 |
解答:
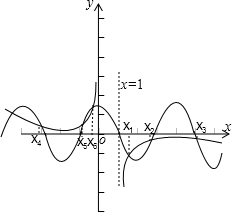 解:令f(x)=0即:cos
解:令f(x)=0即:cos
x+
=0,
则:设y1=cos
x,y2=-
,
在坐标系内画出y1=cos
x 和y2=-
的图象图象有6个交点,
其中有三对都关于x=1对称,
所以x1+x2+x3+x4+x5+x6=6,
故答案为:6
 解:令f(x)=0即:cos
解:令f(x)=0即:cos| π |
| 2 |
| 1 |
| x-1 |
则:设y1=cos
| π |
| 2 |
| 1 |
| x-1 |
在坐标系内画出y1=cos
| π |
| 2 |
| 1 |
| x-1 |
其中有三对都关于x=1对称,
所以x1+x2+x3+x4+x5+x6=6,
故答案为:6
点评:本题考查的知识要点:函数的零点的求法,函数的图象的对称问题

练习册系列答案
相关题目
已知y=f(x)在(0,3)上是增函数,函数f(x+3)是偶函数,则( )
A、f(
| ||||
B、f(
| ||||
C、f(4)<f(
| ||||
D、f(
|
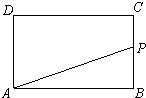 如图,在长为4、宽为2的矩形ABCD上有一点P,沿折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).
如图,在长为4、宽为2的矩形ABCD上有一点P,沿折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).