题目内容
已知椭圆C:
+
=1(a>b>0),F1,F2分别为C的左右焦点,|F1F2|=2
,且离心率e=
.
(1)求椭圆C的方程;
(2)设过椭圆右焦点F2的直线l和椭圆交于两点A,B,是否存在直线l,使得△OAF2与△OBF2的面积比值为2?若存在,求出直线l的方程;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)设过椭圆右焦点F2的直线l和椭圆交于两点A,B,是否存在直线l,使得△OAF2与△OBF2的面积比值为2?若存在,求出直线l的方程;若不存在,说明理由.
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)利用焦距概念和离心率公式,从而求出参数a、b、c,得到椭圆的方程;
(2)假设存在,将条件中的面积比转化为向量关系,得到两点纵坐关系,再通过直线和椭圆联立方程组,得到两点的纵坐标关系,从而求出参数k,得到直线l的方程,说明其存在性.
(2)假设存在,将条件中的面积比转化为向量关系,得到两点纵坐关系,再通过直线和椭圆联立方程组,得到两点的纵坐标关系,从而求出参数k,得到直线l的方程,说明其存在性.
解答:
解:(1)由于|F1F2|=2
,且离心率e=
,
则c=
,
=
,即有a=2,b=
=1,
则椭圆方程为
+y2=1;
(2)假设存在直线l,使得△OAF2与△OBF2的面积比值为2.
则∵△OAF2与△OBF2的面积比值为2,
∴由三角形的面积公式可得,AF2:BF2=2,
则
=2
,
设A(x1,y1),B(x2,y2),
则(
-x1,-y1)=2(x2-
,y2),
∴y1=-2y2 ①
设直线l的方程为x=ky+
,
由
,得到(k2+4)y2+2
ky-1=0,
则y1+y2=-
②
y1y2=-
③
由①②③得k=±
,
因此存在直线l:x=±
y+
,
使得△OAF2与△OBF2的面积比值为2.
| 3 |
| ||
| 2 |
则c=
| 3 |
| c |
| a |
| ||
| 2 |
| a2-c2 |
则椭圆方程为
| x2 |
| 4 |
(2)假设存在直线l,使得△OAF2与△OBF2的面积比值为2.
则∵△OAF2与△OBF2的面积比值为2,
∴由三角形的面积公式可得,AF2:BF2=2,
则
| AF2 |
| F2B |
设A(x1,y1),B(x2,y2),
则(
| 3 |
| 3 |
∴y1=-2y2 ①
设直线l的方程为x=ky+
| 3 |
由
|
| 3 |
则y1+y2=-
2
| ||
| k2+4 |
y1y2=-
| 1 |
| 4+k2 |
由①②③得k=±
2
| ||
| 23 |
因此存在直线l:x=±
2
| ||
| 23 |
| 3 |
使得△OAF2与△OBF2的面积比值为2.
点评:本题考查了三角形面积公式、椭圆的焦距和离心率公式、韦达定理,以及化归转化的数学思想,有一定的探索性,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
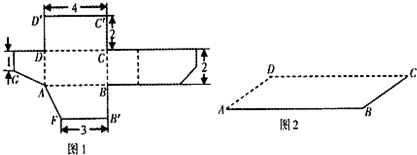 某长方体截去一个三棱锥后,形成的几何体的平面展开图的一部分如图1所示.
某长方体截去一个三棱锥后,形成的几何体的平面展开图的一部分如图1所示.