题目内容
设函数f(x)=x(1+x)2,x∈(-∞,0],
(1)求f(x)的极值点;
(2)对任意的a<0,以F(a)记f(x)在[a,0]上的最小值,求k=
的最小值.
(1)求f(x)的极值点;
(2)对任意的a<0,以F(a)记f(x)在[a,0]上的最小值,求k=
| F(a) |
| a |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:(1)求导f′(x)=(1+x)2+2x(1+x)=(1+x)(1+3x);从而确定函数的单调性及极值点;
(2)由(1)判断f(x)在[a,0]上的单调性,从而求f(x)在[a,0]上的最小值,从而得到F(a),从而求得k=
,再求最小值.
(2)由(1)判断f(x)在[a,0]上的单调性,从而求f(x)在[a,0]上的最小值,从而得到F(a),从而求得k=
| F(a) |
| a |
解答:
解:(1)f′(x)=(1+x)2+2x(1+x)=(1+x)(1+3x);
由f′(x)=0解得:x1=-1,x2=-
;
当x<-1或x>-
时,f′(x)>0;
当-1<x<-
时,f′(x)<0;
所以,f(x)有两个极值点:
x1=-1是极大值点,f(-1)=0;
x2=-
是极小值点,f(-
)=-
.
(2)过点(-
,-
)做直线y=-
,与y=f(x)的图象的另一个交点为A(x,-
),
则-
=x(1+x)2,即27x3+54x2+27x+4=0;
已知有解x=-
,则(3x+1)(9x2+15x+4)=0;
解得A(-
,-
);
当a<-
时,F(a)=f(a);k=
=(1+a)2>
;
当-
≤a≤-
时,F(a)=-
,k=
≥
=
,
其中当a=-
时,k=
;
当-
<a<0时,F(a)=f(a),k=
=(1+a)2>
;
所以,对任意的a<0,k的最小值为
;
(其中当a=-
时,k=
).
由f′(x)=0解得:x1=-1,x2=-
| 1 |
| 3 |
当x<-1或x>-
| 1 |
| 3 |
当-1<x<-
| 1 |
| 3 |
所以,f(x)有两个极值点:
x1=-1是极大值点,f(-1)=0;
x2=-
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
(2)过点(-
| 1 |
| 3 |
| 4 |
| 27 |
| 4 |
| 27 |
| 4 |
| 27 |
则-
| 4 |
| 27 |
已知有解x=-
| 1 |
| 3 |
解得A(-
| 4 |
| 3 |
| 4 |
| 27 |
当a<-
| 4 |
| 3 |
| f(a) |
| a |
| 1 |
| 9 |
当-
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
-
| ||
| a |
-
| ||
-
|
| 1 |
| 9 |
其中当a=-
| 4 |
| 3 |
| 1 |
| 9 |
当-
| 1 |
| 3 |
| f(a) |
| a |
| 1 |
| 9 |
所以,对任意的a<0,k的最小值为
| 1 |
| 9 |
(其中当a=-
| 4 |
| 3 |
| 1 |
| 9 |
点评:本题考查了导数的综合应用及分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
下列函数中,在其定义域上为奇函数的是( )
| A、y=ex+e-x | ||
B、y=-
| ||
| C、y=tan|x| | ||
D、y=ln
|
为了得到函数y=lg(x+3)-1的图象,只需把函数y=lgx的图象上所有的点( )
| A、向左平移3个单位长度,再向上平移1个单位长度 |
| B、向右平移3个单位长度,再向上平移1个单位长度 |
| C、向左平移3个单位长度,再向下平移1个单位长度 |
| D、向右平移3个单位长度,再向下平移1个单位长度 |
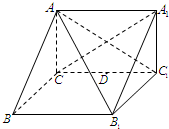 如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.
如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.