题目内容
先将函数y=f(x)的图象向右移
个单位,再将所得的图象作关于直线x=
的对称变换,得到y=sin(-2x+
)的函数图象,则f(x)的解析式是( )
| π |
| 6 |
| π |
| 4 |
| π |
| 3 |
A、y=sin(-2x+
| ||
B、y=sin(-2x-
| ||
C、y=sin(2x-
| ||
D、y=sin(2x+
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:设函数为y=g(x)的图象与函数y=sin(-2x+
)的图象关于直线x=
对称,可求得函数y=g(x)的解析式,继而可得f(x)的解析式.
| π |
| 3 |
| π |
| 4 |
解答:
解:设函数为y=g(x)的图象与函数y=sin(-2x+
)的图象关于直线x=
对称,
则g(x)=sin[-2(
-x)+
]=sin(2x-
),
∴f(x)=g(x+
)=sin[2(x+
)-
]=sin(2x-
),
故选:C.
| π |
| 3 |
| π |
| 4 |
则g(x)=sin[-2(
| π |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
∴f(x)=g(x+
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
故选:C.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查逆向思维与运算求解能力,属于中档题.

练习册系列答案
相关题目
sin15°sin105°的值是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知x,y∈R*,且x+y+
+
=5,则x+y的最大值是( )
| 1 |
| x |
| 1 |
| y |
| A、3 | B、3.5 | C、4 | D、4.5 |
若函数g(x)=asinxcosx(a>0)的最大值为
,则函数f(x)=sinx+acosx的图象的一条对称轴方程为( )
| 1 |
| 2 |
| A、x=0 | ||
B、x=-
| ||
C、x=-
| ||
D、x=-
|
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则f(x)在R上的表达式是( )
| A、y=x(x-2) |
| B、y=x(|x|-1) |
| C、y=|x|(x-2) |
| D、y=x(|x|-2) |
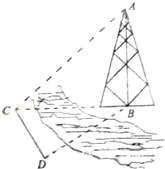 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=60°,∠BDC=75°,CD=50
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=60°,∠BDC=75°,CD=50 如图所示,把一些长度均为4米(PA+PB=4米)的铁管折弯后当作骨架制作“人字形”帐蓬,根据人们的生活体验知道:人在帐蓬里“舒适感”k与三角形的底边长和底边上的高度有关,设AB为x,AB边上的高PH为y,则k
如图所示,把一些长度均为4米(PA+PB=4米)的铁管折弯后当作骨架制作“人字形”帐蓬,根据人们的生活体验知道:人在帐蓬里“舒适感”k与三角形的底边长和底边上的高度有关,设AB为x,AB边上的高PH为y,则k