题目内容
20.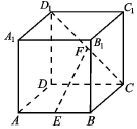 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.(1)求证:EF∥平面ADD1A1;
(2)AB=2,求三棱锥D1-DEF的体积.
分析 (1)取DD1中点M,连接MA,MF,推导出AEFM是平行四边形,从而EF∥AM,由此能证明EF∥平面ADD1A1.
(2)三棱锥D1-DEF的体积${V_{{D_1}-DEF}}={V_{E-{D_1}DF$.由此能求出结果.
解答 证明:(1)取DD1中点M,连接MA,MF,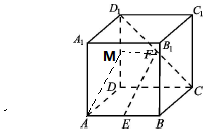
∵正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
∴$MF\underline{\underline∥}AE\underline{\underline∥}\frac{1}{2}DC$,
∴AEFM是平行四边形,∴EF∥AM,
又AM?平面ADD1A1,EF?平面ADD1A1,
∴EF∥平面ADD1A1.
解:(2)∵AB=2,
∴三棱锥D1-DEF的体积:
${V_{{D_1}-DEF}}={V_{E-{D_1}DF}}=\frac{1}{3}{S_{△{D_1}DF}}×2=\frac{1}{3}×1×2=\frac{2}{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
10.已知α,β是两个不同平面,直线l?β,则“α∥β”是“l∥α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.书架上有2本不同的语文书,3本不同的数学书,从中任意取出2本,取出的书恰好都是数学书的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
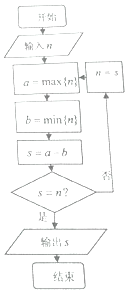 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )