题目内容
5.已知A,B,C是半径为l的圆O上的三点,AB为圆O的直径,P为圆O内一点(含圆周),则$\overrightarrow{PA}$$•\overrightarrow{PB}$$+\overrightarrow{PB}$$•\overrightarrow{PC}$$+\overrightarrow{PC}$$•\overrightarrow{PA}$的取值范围为[-$\frac{4}{3}$,4].分析 根据题意,把$\overrightarrow{PA}$$•\overrightarrow{PB}$$+\overrightarrow{PB}$$•\overrightarrow{PC}$$+\overrightarrow{PC}$$•\overrightarrow{PA}$化为3${\overrightarrow{OP}}^{2}$+2$\overrightarrow{PO}$•$\overrightarrow{OC}$-1,利用参数表示点C(cosα,sinα),P(rcosβ,rsinβ)且0≤r≤1;根据三角函数的有界性求出3${\overrightarrow{OP}}^{2}$+2$\overrightarrow{PO}$•$\overrightarrow{OC}$-1的最值即可.
解答 解:根据题意,$\overrightarrow{OA}$=-$\overrightarrow{OB}$,且|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=1,
∴$\overrightarrow{PA}$$•\overrightarrow{PB}$$+\overrightarrow{PB}$$•\overrightarrow{PC}$$+\overrightarrow{PC}$$•\overrightarrow{PA}$=($\overrightarrow{PO}$+$\overrightarrow{OA}$)•($\overrightarrow{PO}$+$\overrightarrow{OB}$)
+($\overrightarrow{PO}$+$\overrightarrow{OB}$)•($\overrightarrow{PO}$+$\overrightarrow{OC}$)+($\overrightarrow{PO}$+$\overrightarrow{OC}$)•($\overrightarrow{PO}$+$\overrightarrow{OA}$)
=3${\overrightarrow{PO}}^{2}$+2$\overrightarrow{PO}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$)+$\overrightarrow{OA}$•$\overrightarrow{OB}$+($\overrightarrow{OB}$+$\overrightarrow{OA}$)•$\overrightarrow{OC}$
=3${\overrightarrow{OP}}^{2}$+2$\overrightarrow{PO}$•$\overrightarrow{OC}$-1,
以点O为坐标原点,建立直角坐标系,
设点C(cosα,sinα),点P(rcosβ,rsinβ),且0≤r≤1;
则3${\overrightarrow{OP}}^{2}$+2$\overrightarrow{PO}$•$\overrightarrow{OC}$-1=3r2-2rcos(α-β)-1,
∴3${\overrightarrow{OP}}^{2}$+2$\overrightarrow{PO}$•$\overrightarrow{OC}$-1≤3r2+2r-1≤4,
且3${\overrightarrow{OP}}^{2}$+2$\overrightarrow{PO}$•$\overrightarrow{OC}$-1≥3r2-2r-1≥-$\frac{4}{3}$;
∴$\overrightarrow{PA}$$•\overrightarrow{PB}$$+\overrightarrow{PB}$$•\overrightarrow{PC}$$+\overrightarrow{PC}$$•\overrightarrow{PA}$的取值范围是[-$\frac{4}{3}$,4].
故答案为:[-$\frac{4}{3}$,4].
点评 本题考查了平面向量的数量积和利用坐标表示向量以及三角函数的性质与应用问题,是难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3,3 | B. | -3,3 | C. | 3,3i | D. | -3,3i |
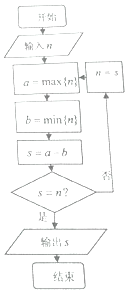 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )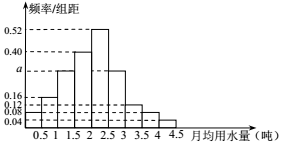 我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.