题目内容
设U=R，P={x|x＜1}，Q={x|x2≥4}，则P∩∁UQ=（ ）
| A、{x|-1＜x＜2} |
| B、{x|-2＜x＜1} |
| C、{x|1＜x＜2} |
| D、{x|-2＜x＜2} |
考点：交、并、补集的混合运算
专题：集合
分析：求出集合Q，利用集合的基本运算即可得到结论．
解答：
解：Q={x|x2≥4}={x|x≥2或x≤-2}，
则∁UQ={x|-2＜x＜2}，
则P∩∁UQ={x|-2＜x＜1}，
故选：B
则∁UQ={x|-2＜x＜2}，
则P∩∁UQ={x|-2＜x＜1}，
故选：B
点评：本题主要考查集合的基本运算，利用条件求出集合Q的元素是解决本题的关键，比较基础．
练习册系列答案
相关题目
已知集合A={y丨y=x2}，B={x丨
＜0}，求A∩B=（ ）
| x+1 |
| x-2 |
| A、[0，+∞） |
| B、（-1，2） |
| C、[0，2） |
| D、（-1，0] |
将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是（ ）
| A、4π | B、3π | C、2π | D、π |
已知全集U={x∈N*丨-1≤x≤7}，集合M={2，4，6}，P={3，4，5}，那么集合∁U（M∪P）是（ ）
| A、{-1，0，1，7} |
| B、{1，7} |
| C、{1，3，7} |
| D、∅ |
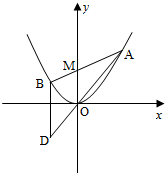如图，已知抛物线C：x2=4y，过点M（0，2）任作一直线与C相交于A，B两点，过点B作y轴的平行线与直线AO相交于点D（O为坐标原点）．