题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，若a2=b（b+c），并且a=
b，判断△ABC的形状．
| 3 |
考点：三角形的形状判断
专题：计算题,解三角形
分析：利用a2=b（b+c），并且a=
b，求出c=2b，可得a2+b2=c2，即可判断△ABC的形状．
| 3 |
解答：
解：∵a2=b（b+c），并且a=
b，
∴3b2=b（b+c），
∴c=2b，
∴a2+b2=c2，
∴△ABC是直角三角形．
| 3 |
∴3b2=b（b+c），
∴c=2b，
∴a2+b2=c2，
∴△ABC是直角三角形．
点评：本题考查三角形的形状判断，考查学生的计算能力，正确运用勾股定理是关键．
练习册系列答案
阅读快车系列答案
相关题目
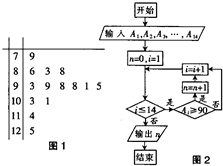如图1是某高三学生14次数学考试成绩的茎叶图，现将该14个数据依次记为A1，A2，…A14，并输入如图2所示的一个算法流程图，那么该算法流程图运行结束时输出的n值是（ ）| A、9 | B、10 | C、11 | D、12 |
设全集U=R，集合A={x|0＜x≤2}，B={x|x＜1}，则集合∁U（A∪B）=（ ）
| A、（-∞，2] |
| B、（-∞，1] |
| C、（2，+∞） |
| D、[2，+∞） |