题目内容
已知函数f(x)=sin2(x)-2(a-1)sinx•cosx+5cos2(x)+2-a,试推断是否存在常数a,使f(x)的最大值为6?若存在,求出a值:若不存在,说明理由.
考点:三角函数的最值
专题:三角函数的求值
分析:利用三角恒等变换化简函数的解析式为f(x)=5-a+(1-a)sin2x+2cos2x,再根据asinx+bcosx的最大值为
、以及题中条件求得a的值.
| a2+b2 |
解答:
解:函数f(x)=sin2(x)-2(a-1)sinx•cosx+5cos2(x)+2-a
=1-(a-1)sin2x+4•
+2-a=5-a+(1-a)sin2x+2cos2x.
故函数f(x)的最大值为 5-a+
=6,即
=1+a,
求得a=1,故存在常数a=1,使f(x)的最大值为6.
=1-(a-1)sin2x+4•
| 1+cos2x |
| 2 |
故函数f(x)的最大值为 5-a+
| (1-a)2+22 |
| (1-a)2+22 |
求得a=1,故存在常数a=1,使f(x)的最大值为6.
点评:本题主要考查三角恒等变换,利用了asinx+bcosx的最大值为
,属于中档题.
| a2+b2 |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
非零向量
,
满足
•
-2
2
2=0,|
|+|
|=1,则
与
的夹角的最小值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
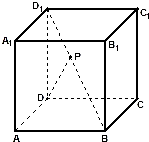 如图,点P在正方体ABCD-A1B1C1D1 的对角线BD1上,且cos∠PDA=
如图,点P在正方体ABCD-A1B1C1D1 的对角线BD1上,且cos∠PDA=
| ||
| 4 |
| A、75° | B、60° |
| C、45° | D、30° |
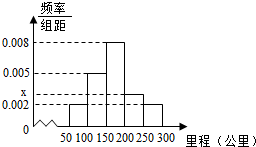 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.